以函数解析式为载体考查函数零点问题，三个学校都在这样命题

2019届浙江杭州第四中学的填空题的压轴题，考查了以函数解析式求法为载体，考查函数的零点问题。首先来看看这道题

来看看此题

本题考查以函数载体解析式为载体考查了，函数的零点问题。

借此题时首先先抓题眼，1 函数单调性，2 f【】=3为定值，3 方程的根

根据前两者题眼，可以快速索定通过换元+待定法求函数解析式，通过此法求出函数解析式后就比较容易了。

方程的根，从函数与方程的关系来求解

由于此函数是超越函数，所以画函数图像只能通过导数法来求

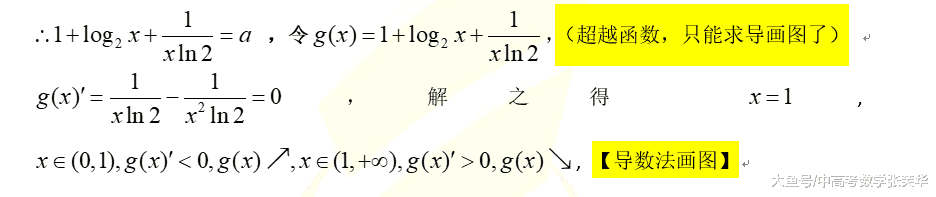
导数法画图时主要找函数的单调性，极值，最值，零点

这道题可以很容易找到函数的极小值也是最小值，当然此题这还不是重点，重点在于最小值两侧函数的变化趋势，此时主要考查函数的极限思想。看到此处是不是感觉很难，是的，此极限思想是江苏高考数学常考的数学思想，所以我们在解题时一定要注意这个解题技巧。

如果想要彻底解决此类问题，张老师给大家总结归纳了一张导图大家可以看看哦。掌握此导图可以彻底解决此类问题

当然这道题，以前张老师视频就讲过哦

当然这类问题2019届河北衡水中学高三第一次大联考也考察了哦

我们也来瓢两眼看看哦

这道题考查了，除了考查了函数的解析式求解外，主要考查了零点定理在解题中的作用

当然除了河北还有一个省份也考了。

看到了码：广西中学也考了哦。不过这道题主要考查导数的运算和几何意义

好了今天张老师就分享到这里

如果感觉有帮助请关注张老师的大鱼号，中高考数学张芙华