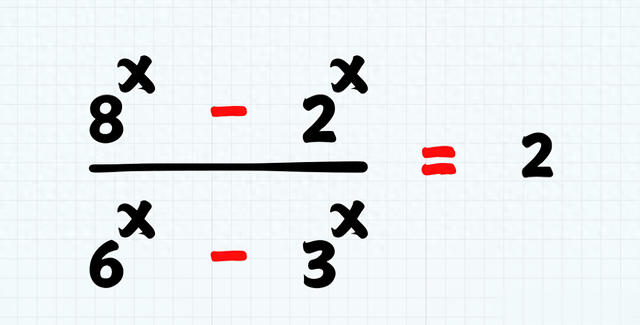
没有两个数字满足这个等式；通过检查，你可以找出满足这个等式的单个数字。

许多人在遇到这个问题时可能会考虑的一种方法是交叉相乘。但这种策略可能会导致复杂情况，并可能让你走进死胡同。

挑战在于，假设x是一个整数，找到x的所有可能值。

你会用什么方法来解决这个问题？

提示：表达分子和分母，使得它们有一个共同的因子，可以抵消它，从而得到一个不太复杂的等式。

拿起笔和纸，尝试一下。我很想在评论中看到你的方法。如果你做对了，就击掌！但如果做错了，也不要着急——跟着做就行了。

如果这个挑战引起了你的兴趣，请查看下面的其他谜题列表！

你准备好了吗？让我们开始吧！

仔细看看等式的左边。我们可以从分子和分母得出一个共同点。

我们开始吧！

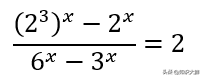
伟大的！

我们再做一件事。

太棒了！我们可以看到2^x是等式中非常常见的项。这告诉我们可以继续进行因式分解。

分解因式后，我们得到：

仔细观察；我们可以将 ( 2^x)²-1转换为两个平方差的表达式。

太棒了！你在想什么？

现在分子和分母中都有一个共同项。让我们将其抵消吧！

这给我们留下了：

伟大的！

此时，我们可以通过交叉相乘得到线性表达式。

让我们除以 2。结果如下：

太神奇了！还有一件事。仔细看看这个等式，任何大于或等于 2 的值都会使这个等式无效。为什么？

左侧永远是 2 的因数，这意味着它永远是偶数。另一方面，无论x的值是多少，右侧永远是奇数。

任何等式要想成立，等式的两边都必须是奇数或偶数。

请记住， x的值是整数。这也意味着任何小于或等于 -1 的数字都不满足该等式。

我们还剩下哪些范围的价值观？

0，显然不满足方程。

那1呢？让我们看看！

太棒了！我们找到了！1是唯一满足该等式的整数。