例题1

解法：

设甲村学龄儿童x人。

根据题意，可列方程：100x+550=120x-630。

解得x=59。

现有资金：100×59+550=6450（元）。

额外筹集后资金：6450+2510=8960（元）。

根据“按80元/人的标准”，可分给：8960÷80=112（人）。

乙村学龄儿童有112-59=53人。

因此，选择B选项。

例题2

解法：

根据“高校某专业70多名毕业生中，有96%在毕业后去西部省区支援国家建设”，可知：96%=24/25，说明毕业生总数是25的倍数，即75人。

毕业后去西部省区支援国家建设的毕业生数有：75×24/25=72（人）。

根据“去偏远中小学支教的毕业生占该专业毕业生总数的20%”，可知：去偏远中小学支教的毕业生数有：75×20%=15（人）。

根据“去偏远中小学支教的毕业生比任职大学生村官的毕业生少2人”，可知：任职大学生村官的毕业生数有：15+2=17（人）。

根据“去偏远中小学支教的毕业生比在西部地区参军入伍的毕业生多1人”，可知：在西部地区参军入伍的毕业生数有：15-1=14（人）。

故去国有企业西部边远岗位工作的毕业生数有：72-15-17-14=26（人）。

因此，选择C选项。

例题3

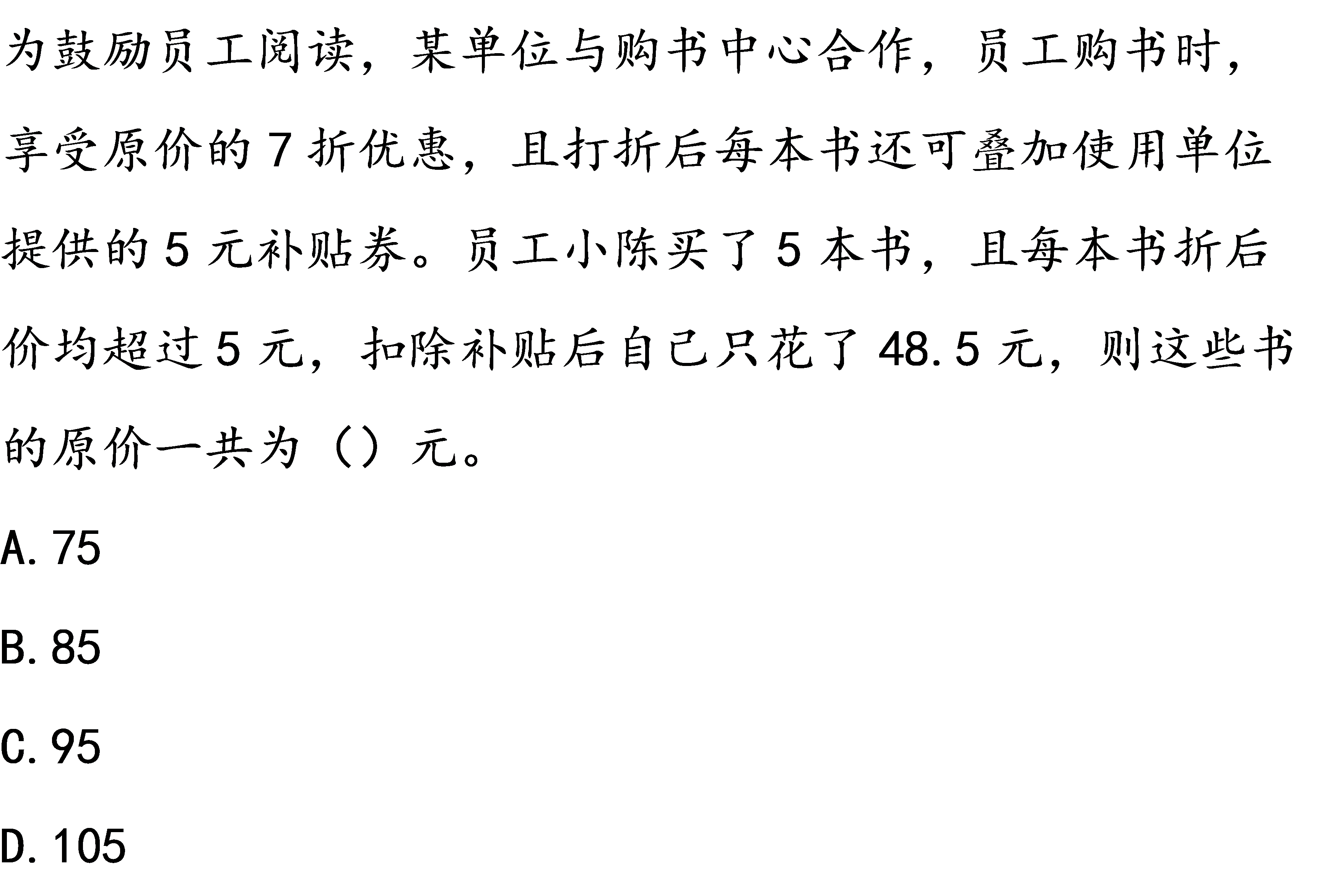
解法：

设这5本书的原价一共为x元，则享受原价的7折优惠价格为0.7x元。

根据“打折后每本书还可叠加使用单位提供的5元补贴券”，可知：5本书再优惠5×5=25（元）。

根据“实际付款48.5元”，可列方程：0.7x-25=48.5。

解得x=105。

因此，选择D选项。

例题4

解法：

根据“9点38分时，甲完成的份数是乙的4倍”，可设9点38分时，乙完成了x份，则甲完成了4x份。

根据“两人每分钟完成分装的份数相同”，可设两人每分钟分装y份。

根据“9点53分时，甲完成的份数是乙的1.5倍”，可列方程：4x+（53-38）y=1.5[x+（53-38）y]。

解得x=3y。

故甲比乙早开始工作（4x-x）÷y=3x÷y=9（分钟）。

因此，选择D选项。

例题5

解法：

设丙村的人数为x人，则甲村的人数为2x人。

根据“每人正好能分24斤”，可知：大米的总量为24×2x=48x（斤）。

设乙村的人数为y人。

根据“第一批大米分给乙村，每人正好能分12斤，第二批大米分给甲、乙、丙三个村，每人正好能分4斤”，可列方程：12y+4（2x+y+x）=48x。

化简得：y=2.25x。

故乙村人数为2.25x人。

根据“将两批大米都分给乙、丙两村”，可知：每人可分48x÷（y+x）=48x÷（2.25x+x）=192/13≈14.8（斤）。

因此，选择B选项。