我认为这个问题很好地测试了数学技能。我还记得一道类似的 3D 问题，那是我大学 A-level 课程的祸根。

现在进行设置。点位于 (4, 4)。蓝线方程为y = 2 x。

该点与线的距离是多少？水平方向距离为 2，但我们追求最短距离。图片应该会提示您如何做到这一点。

尝试一下吧——解决方案就在下面，后面还有一些额外的挑战。

从(4, 4) 到y = 2 x的最短路径是沿着与y = 2 x垂直的线。计划如下：

一个有用的数学事实是，两条垂直线的梯度乘积总是 -1。要得到 -1，我们需要将 2 乘以 -1/2，因此新线的梯度为 -1/2。

红色的新垂直线

红线的形式为y = (-1/2) x + c。为了找到c，我们将插入我们知道该线经过的一个点，即 (4, 4)。

y = (-1/2) x + 6. 为了找到这条线与y = 2 x的交点，我们将它们相等。

6 = 2.4 * 2.5。这很漂亮。无论如何，这两条线在 (2.4, 4.8) 处相交，因此剩下的就是找到 (2.4, 4.8) 和 (4, 4) 之间的距离。

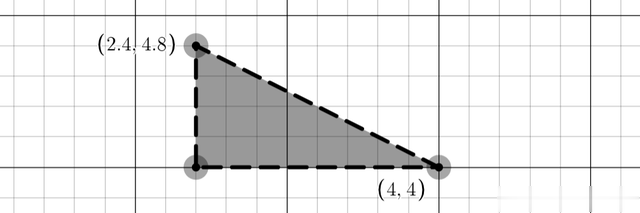
如您所见，我们可以利用毕达哥拉斯定理快速完成此操作。

距离是

这样就解决了问题。✅

挑战 1 ：找出 (4, 4) 与直线y = 2 x + 1之间的距离。

挑战 2 ：找出 (4, 4) 与曲线y = x² + 2之间的距离。