甲、乙两个瓶子共有水600克，从甲瓶子取出1/4，从乙瓶子取出1/5，结果两个瓶子共剩下2000克。问：两个瓶子原来各有多少水?

一、看一看

分析题目中的数量关系：

1. 共有水2600克。

2. 甲取出1/4。

3. 乙取出1/5。

4. 一共剩下2000克。

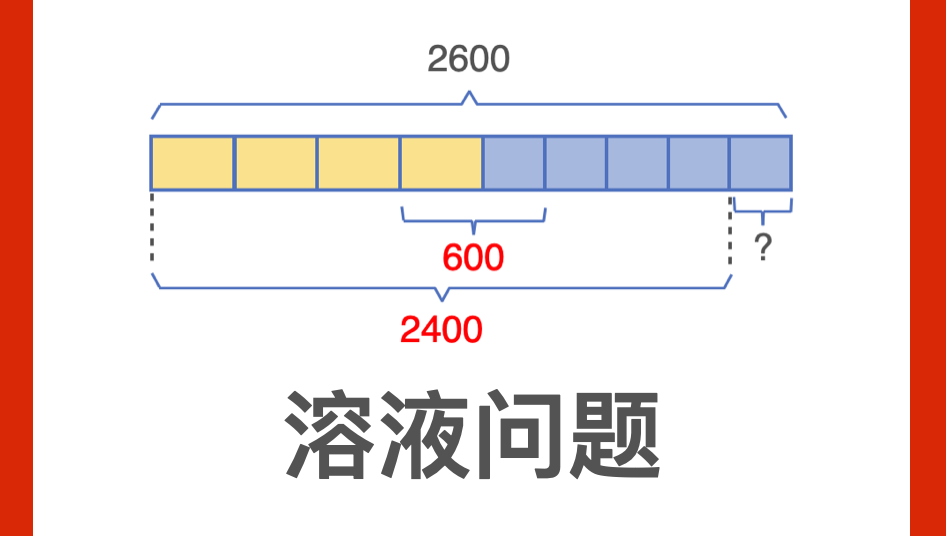
二、画一画

甲乙容器的溶液各分为4份和5份。

1. 甲瓶子画4份，乙瓶子画5份，一共是2600克。

2. 甲1份加上乙1份的量是2600减去2000等于600克。

3. 甲4份加上乙4份一共2400克。

4. 剩余乙1份是2600减去2400等于200克。

5. 乙是5份，一共是1000克。

6. 甲是4份，一共是1600克。

三、算一算

1. 甲瓶子1600克加上乙瓶子1000克一共是2600克。

2. 甲瓶子1/4是400克，乙瓶子1/5是200克，加在一起是600克。

解答完毕之后，答案的正确与否还需要去检验，一个个代入题目中，看是否满足已有的条件。这一步至关重要，很多孩子解答后没有代入题目中，就有可能会出错。

四、想一想

通过画出各自份数，可以看出甲1份+乙1份对应的数量关系。

建模思维的核心就是找出题目中的最小量、不变量或总数作为几份量，画出它们之间的数量关系。

五、新加坡小学数学建模

新加坡数学建模是一种可视化的思维，它将抽象的数量关系转化为直观图形，帮助学生在脑海中构建桥梁，通过具体形象，如○、□，线段等，让孩子们能更直观地理解“相差关系”等数学关系。这种能力的早期培养，为高年级学习中遇到的复杂概念和问题提供直观理解的基础，并且可以让孩子平滑的过渡到初中方程思维。

#新加坡数学建模 #小学数学思维 #小升初数学培优