
航空作家兼研究员大卫·诺兰的一项研究表明,坐在商用飞机的后排在空难中会增加幸存的概率。
研究认为每个座位的幸存概率是不一样的,因此拟合优度检验会拒绝原假设,即每个座位的乘客幸存率都相等。根据 1971 年以后发生的 20 起商用飞机坠机的分析结果,商务舱或头等舱的幸存率为 49%,经济舱中间或者前面的幸存率为 56%,而经济舱尾部的幸存率为 69%。
大卫·诺兰表示他并不会刻意坐在机舱的尾部,因为发生空难的可能性很低。他更喜欢靠窗的座位。
频数分布表
核心概念:在处理大型数据集时,频数分布表(或称为频数表)通常有助于整理和汇总数据。频数分布表能帮助我们理解数据集分布的特点。此外,构建频数分布表通常是构建直方图的第一步,而直方图是用于数据分布可视化的图表。
频数分布表(或频数表)是通过展示数据类别(或组)以及每个类别中数据值的数量(频数),来显示数据是如何在不同类别(或组)间划分的。
构建频数分布表的流程
构建频数分布表的目的是:①汇总大型数据集;②查看数据分布;③识别异常值;④为构建图
表(如直方图)提供基础。频数分布表可以使用统计软件生成,也可以通过如下步骤手动构建。
1. 选择分组的数目,通常在 5 到 20 之间。组数的选择有时需要考虑使用近似值是否方便(根据“斯透奇斯规则”,最佳组数的选择可以依据 1+(logn)/(log2) 近似,其中 n 是数据的个数。
2. 计算组距:

对结果取整,以便得到一个方便使用的数字(通常向上取整)。使用特定的组数不是最为关键的,而更需要关注的是通过更改组数得到方便使用的组上下限。
3. 选择最小值或低于最小值的某一个较为方便使用的值作为第一组的下限。
4. 通过第一组的下限与组距,得到其他组的下限(用第一组的下限加组距得到第二组的下限;用第二组的下限加组距得到第三组的下限,以此类推)。
5. 在一个数列中列出所有组的下限,然后确定并列出所有组的上限。
6. 求得每组的频数。
在构建频数分布表时,要确保各组之间不重叠,即每个原始值只属于其中一个组。即便是那些频数为 0 的组,也要包含在内进行统计。另外,尽可能对所有的组使用相同的宽度,但有时也不可避免地需要使用开区间,如“65 岁或以上”。
空难原因频数分布表
表 2-3 中列出了从 1960 年到最近几年有关空难原因的数据。数据是名目测量尺度下的分类数据,但也可以创建如表 2-3 所示的频数分布表。可以看到,飞行员失误是空难的主要原因。这些信息有助于美国联邦航空管理局(Federal Aviation Administration)等监管机构制定减少此类事故的策略。

用帕累托图展示空难原因
图2-8展示了基于表2-3的帕累托图。图 2-8 和表 2-3 使用了相同的数据,但图 2-8 能让读者更加鲜明地看到,飞行员失误是空难的最重要原因。另外,图 2-8 并没有严格遵循长条高度从左到右依次递减的要求,而是将“其他原因”的组放置在图的最右边起到可视化的效果。

概率在统计学中的角色
概率在假设检验中起到了关键作用。统计学家根据数据做决策:根据低概率排除偶然发生的可能性。请看以下关于概率的作用和统计学家思维方式的例子。
概率论基础
事件是一个过程的结果或结果的任意集合。简单事件是不能进一步拆分的结果或事件。一个过程的样本空间由所有可能的简单事件组成。也就是说,样本空间由所有不能进一步拆分的结果组成。
计算事件概率的三种常见方法
概率的数学符号
P,表示概率。
A、B、C,表示具体事件。
P(A),表示“事件 A 发生的概率”。
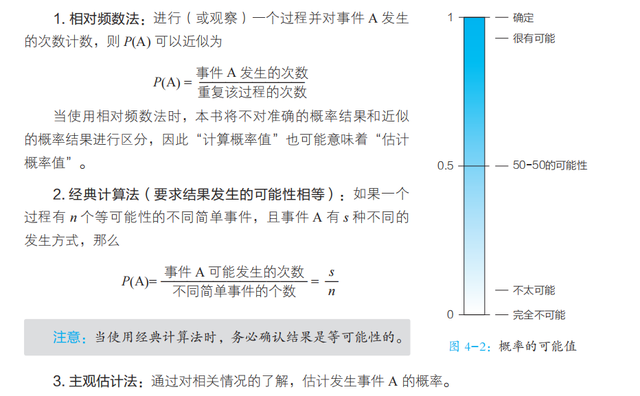
以下是三种计算概率 0 ≤ P(A) ≤ 1 的方法。图 4-2 展示了概率的可能值以及对可能性的描述。
1. 相对频数法:为了确定某类型车辆在一年内发生车祸的概率,我们可以检查过去的结果——一年内正在使用的该类型车辆的数量和该类型车辆的车祸数量;车祸车辆数与总车辆数的比率即为该概率。最近一年,此概率的结果是 0.0480。
2. 经典计算法:假设某彩票游戏的规则是从1~60 个数字中选择 6 个不同的数字,且每种组合出现的概率都是相等的。现在需要确定中头奖的概率。使用 4-4 节展示的方法可以发现,中头奖的概率是 0.0000000200。
3. 主观估计法:假设需要估计被困在电梯里的概率,经验告诉我们,这个概率相当低。因此就估计它为 0.001。
相对频数法
任意给定一个航班,试求其发生空难的概率。假设在最近的一年中,大约有 3900 万个商业航班,其中发生空难 16 次。
解答:使用相对频数法,计算如下:

因为两种结果(空难与没有空难)的可能性是不等的,所以不能使用经典计算法。在没有历史数据的情况下,可以使用主观估计法。
用百分比表示概率?
从数学上讲,概率值 0.25 等于 25%,但是一般使用分数和小数而非百分比是有原因的。在进行概率值计算时(如 0.25×0.25),虽然对小数的处理更为容易,但可能会导致很大的计算问题。专业期刊或统计软件几乎都用小数来表示概率。
使用相对频数法所得的概率是一个近似值,而非确切值。但随着观测次数的增加,相应的近似概率趋于接近实际概率。这个性质通常被称为大数定律。
大数定律:多次重复某个过程,事件的相对频数概率趋于接近实际概率。
大数定律告诉我们,相对频数法往往随着观测次数的增加而会得到更好的概率估计值。该定律反映了一个符合常识的简单概念:仅基于少数几次试验的概率估计可能会有很大的偏差,但如果进行了大量试验,则估计往往会更加准确。
如何理解“可能”?
我们如何解读“可能”、“不可能”或“极不可能”这些词语?美国联邦航空管理局(FAA)对这些词语的解读如下。
可能:每小时飞行中发生该类事件的概率数量级大于或等于 0.00001。在每架飞机的使用寿命中,这样的事件预计会发生几次。
不可能:在 0.00001 或更小的数量级上的概率。此类事件预计不会在某一机型的单架飞机的总使用寿命内发生,但可能在某一机型的所有飞机的总使用寿命内发生。
极不可能:在 0.000000001 或更小的数量级上的概率。这样的事件是几乎不可能发生的,可以等同为没有发生过。


本书特色
《基础统计学(第14版)(双色)》一书通俗易懂、妙趣横生、案例精彩、数据丰富,且连续25年在美国统计类教材排名第一。书中包括统计学在各个学科领域中的关键应用,不限于自然科学、经济学、法学等,任何专业的学生都能在本书中找到与未来工作相关的实际应用。作者花费数千小时收集的真实数据集,配套200多个案例场景生动讲解知识点应用。希望每一位学习统计学的小伙伴来都拥有这本案头宝典。
