「封面」

本篇预计阅读时长7min，难度 🌟🌟🌟

大家好，我是科学羊🐑，这里是数学篇第五季第19篇。

数学不仅是一门科学，更是一种艺术。

它通过简单的概念揭示了深奥的真理。今天，我带大家一起了解下几个著名的数学定理和悖论，包括Brouwer不动点定理、罗素悖论、连续统假设、停机问题以及芝诺的阿基里斯与乌龟悖论。

注意，本篇大家只做了解即可，无需涉入很深。

其实。了解这些概念不仅展示了数学的奇妙之处，还引发了对逻辑、无穷大和计算能力的深刻思考。

废话不多，我们开始～

01 Brouwer不动点定理

让我们先从一个简单的日常例子开始。

你知道吗？当你拿起一杯牛奶，用勺子随意搅拌，无论你如何搅动，总会有至少一个分子保持在原来的位置。

这就是Brouwer不动点定理的一个生动例子。

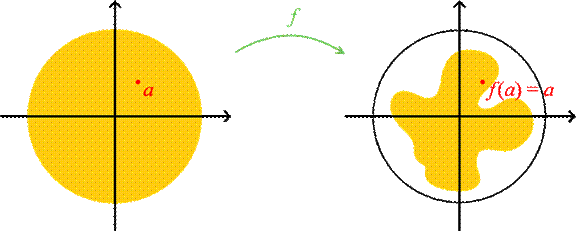
Brouwer不动点定理指出，任何从平面圆到其自身的连续函数必须至少有一个固定点。

也就是说，如下图所示，假设你有一个圆盘，可以把它想象成一张橡皮膜，然后你在上面做一个变形，但这个变形是连续的，比如拉伸或旋转。

无论你怎么变形这个圆盘，总有至少一个点的位置是没有变的，而这个点就是不动点。

数学方式来表述，就是如果你有一个连续函数f，它将一个紧致盘（在二维欧几里得空间中，闭合且有界的圆盘）映射到自身，那么一定存在一个点

x 使得f(x)=x。

这个点 x 就被称为该函数的一个不动点，现在应该很清楚了吧！

为了更好地理解这一现象，我们还可以使用地图来说明。

拿出两张完全相同的地图，把其中一张揉成一个球，放在平铺的第二张地图上。

在揉成球的地图上，总会有至少一个点直接位于平铺地图上对应的点的上方。

从数学角度看，连续函数是一种输入微小变化会导致输出微小变化的函数。换句话说，输入值的小变化不会导致输出值的突变。

Brouwer不动点定理的应用不仅限于简单的物理示例。

它在经济学、工程学和计算机科学中也有广泛应用。例如，在经济学中，这一定理可以用来证明市场均衡的存在性。

02 罗素悖论

接下来，我们来看一个有趣的逻辑悖论——罗素悖论。

假设在一个小镇里，有一个理发师，他给每一个不刮胡子的人刮胡子。那么问题来了：谁给理发师刮胡子？

如果理发师自己刮胡子，那么他就是在给一个自己刮胡子的人刮胡子，这违背了他自己的规则。

如果理发师不刮自己的胡子，那么他就是一个不刮自己胡子的人，所以他应该刮胡子吗？

这种自相矛盾的情况揭示了集合论中的一个重大问题。

罗素悖论指出，如果我们假设存在一个集合R包含所有不包含自己的集合，那么R是否包含自己会导致矛盾。

罗素悖论引发了对集合论的重新评估，最终导致了一致的公理系统的形成，这些系统对集合的形成施加了限制。

德国数学家Ernst Zermelo在1908年提出了第一个公理化系统，后来由以色列数学家Abraham Adolf Fraenkel改进。

这个悖论比较深奥，我们先点到为止，未来再详谈！

03 连续统假设

我们继续探讨另一个令人着迷的数学概念——连续统假设。

想象你是一家拥有无限多个房间的酒店的经理，每个房间都有一个客人。

即使所有的房间都被占用了，酒店仍然可以容纳无限多的新客人，只要新客人的数量与自然数的数量相同。

这个思想实验由数学家大卫·希尔伯特在1924年的讲座中提出，建立在康托对无限数研究的基础上。

希尔伯特通过这个实验表明，不是所有的无限都是相同大小的。

如上图所示，数学家用映射的概念来定义两个无限集合是否相等。

如果两个集合之间可以建立一个双射，即每个集合中的元素一一对应，那么这两个集合的大小相等。

整数集和自然数集之间就可以建立这样的双射，因此它们具有相同的基数，即可数无限。

然而，实数集与自然数集之间不能建立双射，因此实数集的大小（基数）比自然数集大。

这种对不同大小的无限集的研究提出了连续统假设，但至今这一假设仍未得到证实。

04 停机问题

让我们探讨一个与计算机科学密切相关的问题——停机问题。

def output(text):while True:print(text)output("Hello, world!")

请看上面这个程序，您能不能肯定它是否将停止运行或永远持续运行吗？

停机问题问的是，给定一个算法和一个输入，是否可以确定该算法最终会停止运行还是会进入无限循环？

阿兰·图灵在1936年发表的一篇论文中证明，即使是一台拥有无限内存和处理能力的计算机，也无法通过一个通用的算法来确定每个给定的算法/输入对是否会停止运行。

图灵通过一个自我参照的论证证明了这一点。

假设存在一个函数halt()，它接受两个参数——算法A和输入I，并返回True（算法最终停止）或False（算法进入无限循环）。

图灵设置了另一个函数return()，它调用halt()并根据halt()的结果进入不同的状态，从而导致矛盾。

这个悖论表明，存在一些问题，即使我们拥有无限的计算资源，也无法解决。

这些问题对计算能力设定了限制，揭示了计算理论中的一些深刻真理。

05 阿基里斯与乌龟

最后，让我们来看一个古老而有趣的哲学悖论——阿基里斯与乌龟。

5世纪希腊哲学家埃利亚的芝诺提出了这样一个情景：想象士兵阿基里斯和乌龟之间进行赛跑，乌龟在比赛开始时领先。

为了追上并超过乌龟，阿基里斯必须首先到达乌龟的起点。然而，此时乌龟已经向前移动了一段距离。

阿基里斯再次必须走完乌龟走过的路程，但每次他到达乌龟曾经到过的地方，乌龟又前进了一点。

按照芝诺的逻辑，虽然阿基里斯每次所需追赶的距离变得越来越小，但这些距离有无限多，因此阿基里斯需要无限多的时间才能追上乌龟。

这一悖论展示了如何通过对无穷小和无穷大的思考来挑战我们的直觉。

结语

这些数学定理和悖论不仅展示了数学的深奥之处，也引发了对逻辑、无穷大和计算能力的深刻思考。

从Brouwer不动点定理的固定点，到罗素悖论的集合论矛盾，再到连续统假设对不同大小的无限集的探讨，停机问题对计算能力的限制，以及芝诺的阿基里斯与乌龟悖论中的无穷递归，每一个都揭示了数学的独特魅力。

希望通过这些探讨，能让你感受到数学之美，并激发你对数学的进一步兴趣和研究。

无论是在日常生活中还是在科学研究中，数学总能带给我们新的视角和深刻的理解。