天文导航具有特有的优越性是GPS等无线电导航系统无法比拟的。它可以作为独立的一套导航系统。

三视场结构布局在 定位定向方面更为可靠 , 定位定向精度高。三视场系统由于有视场个数的冗余, 当其中某一视场受到杂光或者云层干扰时, 其余视场仍然能够正常工作, 抗干扰能力强;

并且当某一视场指向星点分布比较稀疏的天区, 导致该视场内观测星点数量少而无法完成星图识时, 可以联合其他视场中的星点, 通过三个子星图数据融合的方法完成星图识别进而提高测量的效率。

三视场结构的优点除此之外还有:分视场的视场角可以更小, 以降低天空背景噪音, 并提高测量精度。 故三视场定位定向系统更加健壮。

文中以三视场定位定向设备本身作为研究载体, 采用三视场光学系统结构进行多传感器的测量来完成定位定向。

水平倾角传感器测量水平倾斜角 ρ、τ。 水平倾斜角传感器是商用的全温补高精度数字倾角测量设备, 它的综合精度由大量实验测量确定。 它标称的单轴标准差为0.005° (±10°) 、0.003° (±7°) 、0.001° (±3°) 。由于测量次数不多, 其应符合t分布。水平倾斜角的测量误差会影响到定位定向信息对中

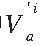
的计算精度。

设备的时间由时间通信系统提供。 在GPS有信号时, 通过GPS校正系统时间。 时间通信系统的精度为10-11s , 而曝光时间锁存的极限误差为4.8 μs 。 由于没有任何可参考的误差模型, 故以均匀分布对待。

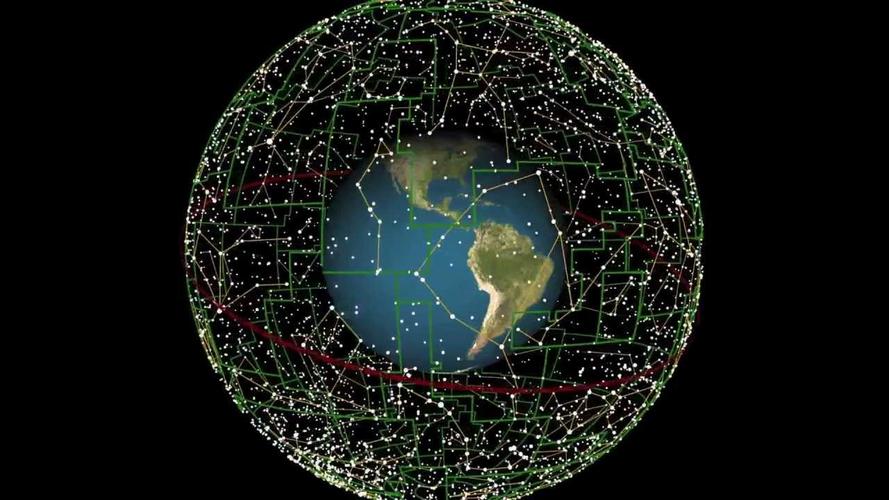
因为67 ms的世界协调时误差会引起恒星在真春分点赤道坐标系下约1″的误差, 故上述时间系统误差引起的恒星矢量Vγ的极限误差为7.2×10-5″ 。 它对恒星位置由Cγ到CTIRS的转换影响也很微弱, 最终对定位定向信息对 中

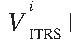
的计算影响在毫角秒的级别,引起的位置误差在1 dm以下。 所以在定位定向的仿真分析中忽略时间误差造成的影响。

温湿压传感器测量大气参数, 用于大气折射校正。 由设备制造商提供, 其标称的误差如下: 温度输出的标 准差为0. 2 ℃ ; 湿度输出的标 准差为2%RH;

大气压测量输出的标准差为0. 3 h Pa 。 大气测量参数符合正态分布。大气参数测量的精度影响大气校正的精度, 对定位定向信息对中

造成影响。

在信噪比为10 d B时, 质心定位在x、y分量方向的标准差为0.051, 符合正态分布 , 此由设备 标定测试时获取。质心提取的精度影响了星角距的计算精度, 进而影响了星图识别。 另外质心提取的精度影响到定位定向信息对中的计算精度。

光学系统 标定参数 包括三个 视场的焦 距fci、 主点、 畸变参数、 光轴在载体中的单 位矢量Axi Veci=[cos (Ai) cos (Ei) , sin (Ai) cos (Ei) , sin (Ei) ]T, 以及探测器安装角。 这些参数由标定获取 , 光学系统参数的标定误差 通过公式2、3传递 , 影响到真值VB的计算。

标定参数的优化值{fci、KPi、Dti、Ai、 Ei、Fix Angi}′ 是通过多个星点组成的 {PtImg, VB} 通过优化分析得到的, 此时由PtImg通过公式2、3可以得到估计值VB′ 。光学系统标定参数的误差可以由估计值VB′ 与真值VB之间关系表示。

通过标定实验数据的合成分析发现:在空间中VB′ 绕着VB在其周围随机分布。 VB与VB′ 之间的角距符合正态分布 , 均值为1.710″ , 标准差为1.153″;VB′ 相对VB的方位角是在 0° , 360° 之间均匀分布 。即估计值VB′ 以VB为轴, 角距差为半径, 在其圆周上随机分布。

极移参数由国际地球自转和参考系服务处提供, 精度可由其发布的公告A给出。 若使用公告A的数据, 那么一般来讲未来40天的预测极移极限误差不超过0.02″, 将其视为均匀分布。自观测以来极移参数范围:xp∈ (-0.4″, 0.4″) , yp∈ (-0.3", 0.6″)。

若无法正确获取公告A的内容则需要将极移参数设置为0, 那么公式6中CTIRS至CITRS的转换矩阵为单位矩阵。 在计算分析中若忽略极移, 则极移数值也是计算的误差源之一。

垂线偏差 (η, ξ) 的数据来 自于美国 国家地理 重力模型开发小组。 其发布了地球重力场EGM2008的数据, 覆盖全球。 其中 η 分量的误差 △η 为正态分布, 且 △η~N (0.663, 0.723) ;ξ 分量的误差 △ξ 也为正态分布 △ξ~N (0.659, 0.724) 。

在计算中采用修正的Bennett大气折射校正公式 , 其极限误差为0.9″, 其误差分布没有参考 , 以均匀分布对待。 它主要影响到蒙气差校正后的恒星矢量

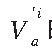
的准确性。

文中恒星位置是在国际天文坐标系框架下, 采用IAU2000B的岁差章动模型计算获得的。 恒星在真春分点赤道坐标系中位置矢量Vγ的计算精度在10-3″, 所以在文中忽略恒星矢量Vγ的计算误差。 不考虑恒星位置的计算对定位定向信息对中

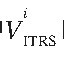
的影响。

表1是影响定位定向的主要误差源。从上述分析中可以看出: 不同的误差源影响到定位定向计算过程中的不通阶段; 对定位定向信息对造成了不同的影响。

误差源对定位定向误差的影响是非线性的, 无法给出明确的数学解析表达式。 此时要确定出哪些误差源对定位定向的影响最大以及造成误差的大小, 采用蒙特卡罗法使用大量随机仿真实验进行误差分析最合适。

在大量随机仿真分析中将不同的误差源添加到仿真计算过程中就可以分析误差源出对定位定向精度的影响。

仿真过程 中三视场 系统的三 个视场大 小均为 [4.5° 3.3750° ]T, 三个视场 的视轴水 平投影间 隔120° , 高度角45° , CCD分辨率为1 024*768 , 像素尺寸为4.65 μm*4.65 μm;主点位置在CCD的靶面中心, 且光学系统无畸变, 极限探测能力为7等星。

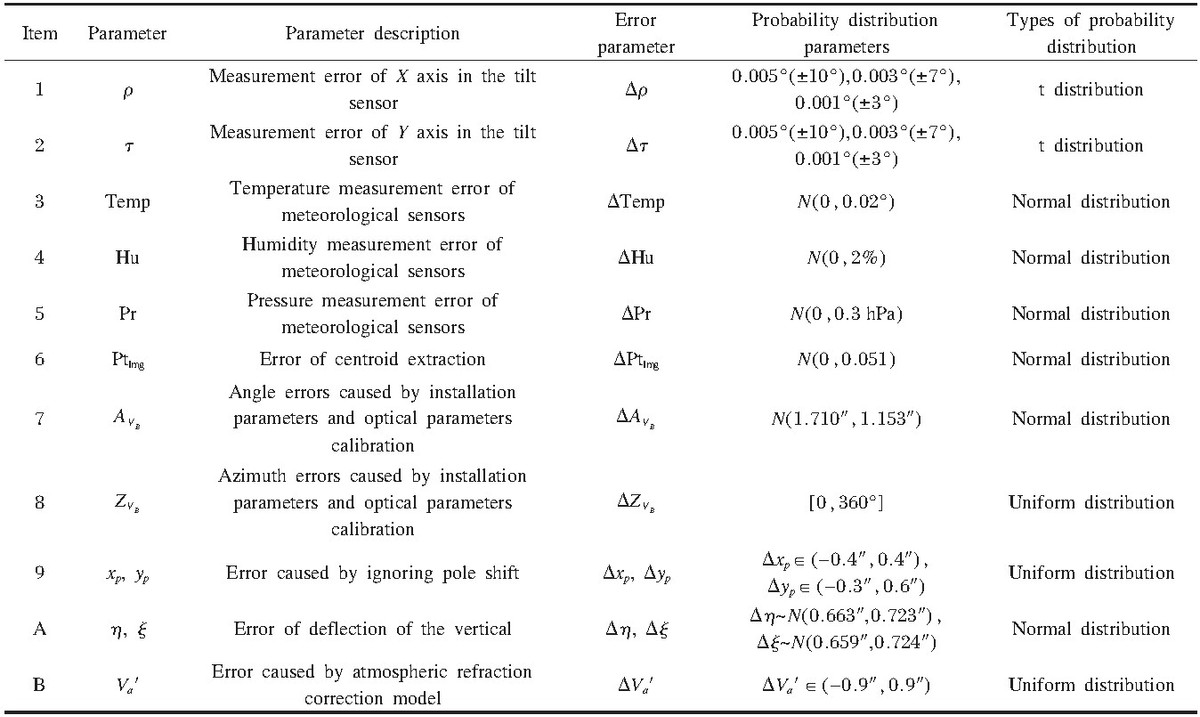
表1 主要误差源的分布特性

采用可见光波段的Tycho2星表作为基本星表, 采用世界协调 时为2013-10-1 0:0:0, 载体平台 的倾角为0° , 0°, 即载体坐标系与水平辅助坐标系重合 。图4是定位定向误差仿真分析的流程图。 其中质心PtImg的计算流程如图5所示。

首先,设置仿真次数Counts=1 000, 每次随机 选取载体平台所在的地理位置Loc,载体平台的方位角Azi作为定位定向真值;其中, 在区间[-180°, 180° ) 上服从均 匀分布 , φ 在区间 [-90° , 90° ] 之间服从均匀分布, Azi在区间[0°, 360°) 上服从均匀分布, h设置为固定的值 , 如200 m 。

其次,根据地理位置、方位角以及三个视场光轴在载体坐标系中的矢量, 通过坐标变换可以计算视轴在国际天球坐标系内的单位矢量Axi Vec ICRS,并据视场大小从星表中提取每个视场内的恒星集合Stari。

图4 定位误差程

由于仿真实验主要是分析三视场定位定向误差, 故仿真忽略星图识别的过程。 直接由时间信息获得恒星 集合在真 春分点赤 道坐标系 内的位置 矢量Vγ,然后计算恒星在TIRS坐标系中的矢量VTIRS, 对其添加 极移误差 计算其在ITRS坐标系内 的矢量VITRS。 它是定位定向信息对的其中一项 。

再次, 计算图4中提取到的恒星集合Stari在图像坐标系内的质心位置。 此质心位置可以通过图5中所示的流程计算得到的, 其实质是星图模拟的过程。

图5中的计算过程中使用的极移参数、地理经纬度和方位、大气参数、水平侧倾角、光学标定参数等都是没有添加误差的,故得到质心位置是无误差的。 然后, 如图4中所示的那样: 对计算出的质量位置PtImg添加各种 误差 , 顺次计算 获得添加 了误差的Va′ 。 它是定位定向信息对的另外一项 。

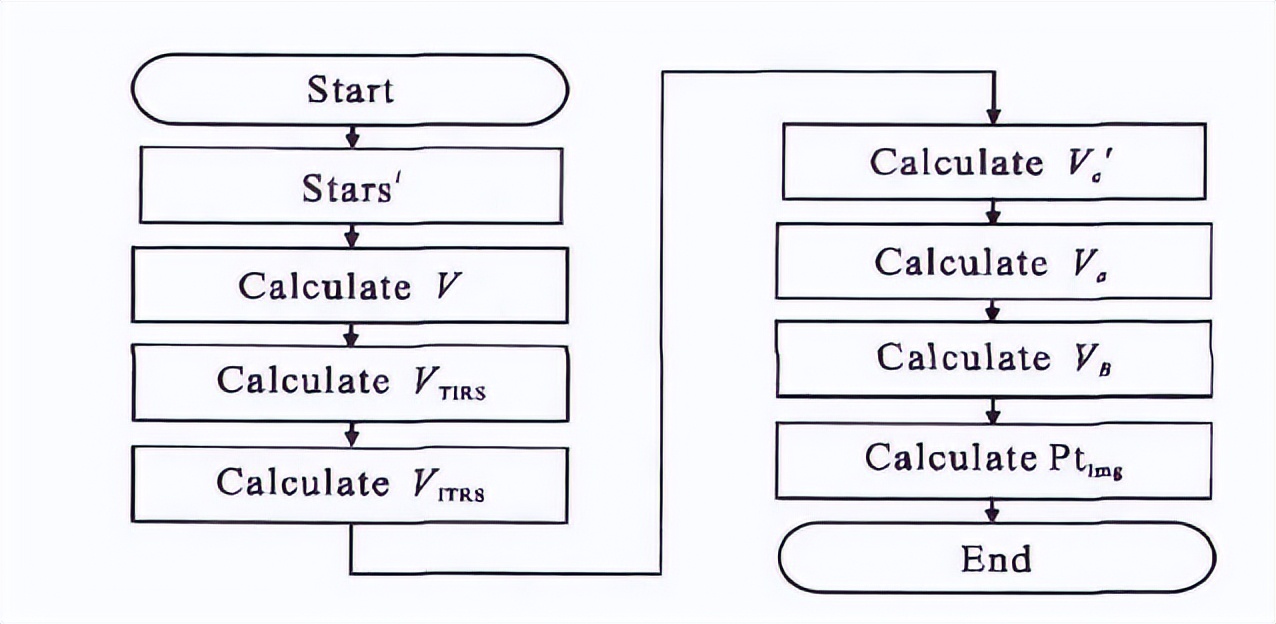
图5 PtImg计算

最后, 由获得的定位定向信息对完成天文学意义上的定位定向, 此定位定向结果需结合垂线偏差数据,获得地理学上意义上的定位定向结果, 即求取到经度 λ′, 纬度 φ′, 方位角Azi′。 它们是上 述真值 λ、φ、Azi的估计值 。

接着通过公式15、16完成定位定向误差的计算。 此时完成一次定位定向, Counts减1。 重复此过程直至Counts为0, 仿真过程结束。

仿真分析中定位和定向误差的计算方法为 :每次仿真 过程中随 机生成真 实的地理 位置Loc 和载体平台的方位角Azi , 与仿真结果Loc 、Azi′ 相对应 。 对于第i次仿真 , 可以获得定位的误差Dist Erri和定向的误差Azi Erri, 计算如下式 :

若仿真分析Counts次, 那么可以获得定位误差的均值MeanDist Err和定向误差的均值MeanAzi Err, 以及定位 误差的平均偏差MeandevDist Er和定向误 差的平均偏差MeandevAzi Err。 平均偏差Mean Dev的定义如下 :

式中:是样本xi的均值。 它与标准差相比对粗大误差的抗干扰能力更强;在数值上和标准差近似。

在野外实验时选 择Imaging Source公司的三 台单色工业CCD相机 , 分辨率为1 024*768, 像素尺寸为4.65 μm*4.65 μm。 光学系统的口径73 mm, 光学视场约为[4.5° 3.3750°]T。

水平倾角传感器的使用范围为±3°, 其他误差源数值与表1一致 , 质心提取 误差的标准差为0.051像素。白天的实验验证需要采用三个大靶面短波红外相机构成红外光学系统进行实验 , 成本高昂 , 故实验平 台选取可 见光波段CCD相机搭建光学系统进行实验验证。

图8 三视位定简易平台

此平台仅适合在夜晚进行观测实验, 但其可以完整验证系统的可行性并完成误差分析。

图8是三视场定位定向设备的实验平台,将其摆放在野外进行实验验证, 平台下部是一个小转台, 三个光轴固定在平台之上, 通过控制转台的转动可以使得平台的姿态随意变换,平台码盘的分辨率为1″ , 通过调整平台可以使其平台的倾角传感器测量值读数为 (0″, 0″) 。

GPS测量的精确地理位置为125° 24′16″E , 43°50′45″N , 200 m, 系统的精确方位角通过北极星校正得出为78.436 7°。

实验过程中, 时间间隔1 s采集一帧星图图像进行定位定向解算, 整个实验过程持续1 000 s。

图9和图10中的2幅图分别为1 000次定位定向实验 的实验结 果 , 对结果进 行统计 :定位误差 为: 232.7 m ,平均偏差为8.1 m , 定向误差 为11.2″ , 平均偏差为2.4″。 在野外定位定向实验中, 水平传感器的测量值误差, 垂线偏差数据的误差是系统的固定误差,它直接影响了测量的最终精度, 并且难易从系统误差中除去。

定位定向的随机误差主要由质心提取的误差、温度造成光学系统参数改变等因素造成的。 通过人工精细微调平台, 标定后使其更加水平。 此时水平倾角传感器读数改变了数角秒。

此时再次重复上述实验, 此时经数据分析得出定位误差为182.12 m, 平均偏差 为7.6 m, 定向误差 为9.3″, 平均偏差 为2.1″ 。 显然载体平台水平倾角传感器的测量误差对结果影响很大。