高分SCI神器 - 限制性立方样条图，可以一键生成了，完美复刻新英格兰杂志风格！

在医学研究领域，限制性立方样条（Restricted Cubic Splines, RCS）是一种常见的统计方法，广泛应用于各类研究中。然而，现有的统计软件在生成 RCS 图像时，通常需要大量的时间和精力来调整参数和外观，以满足高分 SCI 期刊的要求。此外，撰写论文的方法学部分也是一个费时费力的过程。针对这一问题，MSTATA 医学统计机器人推出了一款全新的 APP —— “一键生成限制性立方样条图”，让您能够快速、高效地生成符合高分SCI期刊要求的RCS图像和相应的论文描述。

主要特点：

可以轻松上传科研数据，通过简单的点击设置，即可自动生成限制性立方样条图。

支持线性回归、Logistic回归、Cox回归等多种回归方法。

支持新英格兰医学杂志（NEJM）和美国医学会杂志（JAMA）的图形风格。

能够自动探索曲线的拐点，提高分析准确性。

支持自动用曲线拐点将数据分成两部分，自动进行分段普通回归。

自动生成统计图文报告，包括Objective, methods, 和results等文字描述，大大节省撰写论文的时间。

软件主要引导大家完成三个步骤：

建立RCS曲线，观察形状

寻找RCS曲线的拐点

用拐点切割数据，进行分段普通回归分析

"一键生成限制性立方样条图" APP是一款针对现有统计软件痛点推出的创新应用，旨在为医学研究者提供更高效、便捷的 RCS 生成与论文撰写解决方案。通过自动化的操作，我们的软件为您提供了一种全新的 RCS 生成体验，从而让您专注于研究本身，提高工作效率。让我们的 APP 助力您的科研工作，实现更高水平的学术成果！

立即访问 www.mstata.com，进入MSTATA医学统计机器人 - 以临床研究类型分类 - 影响因素研究 - 限制性立方样条图，开始论文生成之旅。

MSTATA自动生成的论文初稿如下：

软件界面：

生成限制性立方样条图

第一步：先初步生成RCS曲线，观察曲线形状和趋势

这一步先通过设置确定曲线的形状和复杂度，为第二步寻找拐点做准备

选择结局变量

机器人根据结局变量的类型来选择分析方法。二分类变量，纵坐标可选OR或HR。如果是生存变量Time和Status的组合，纵坐标会采用HR。如果是连续性变量，则为Y预测值。

选择影响因素变量

此时只能选择连续性变量作为影响因素X，如果菜单中看不到你想要的变量，请返回设置为numeric

选择协变量

可以调整混杂因素，协变量可以是连续性变量，也可以是分类变量。协变量个数不能超过样本量/20，一般别超过10个，最好做变量筛选以避免多重共线性的影响。

另外，协变量的缺失值也对结果影响很大。应先对协变量进行缺失值填充等处理。

设置knot数

在限制性立方样条（RCS）方法中，knots（节点）是一个关键概念。节点是分布在自变量范围内的一组预定点，用于将三次多项式连接在一起，形成一个连续、光滑的曲线。设置合适数量的节点是非常重要的，因为节点数量的多少会影响模型的灵活性和拟合效果。以下是关于设置节点数量的一些建议：

默认设置：在许多情况下，使用默认的节点数量（通常为3-5个）已经足够应对大多数场景。这可以在不失去太多模型灵活性的同时，避免过拟合的问题。

经验法则：另一种设置节点数量的方法是参考经验法则。根据数据量和复杂性，可以设置不同的节点数量。例如，对于小样本数据集，通常建议使用较少的节点（例如3-4个），而对于大样本数据集，可以尝试使用更多的节点（例如5-7个）。

基于数据驱动的方法：此外，还可以通过交叉验证、Akaike信息准则（AIC）或贝叶斯信息准则（BIC）等数据驱动的方法来选择最优的节点数量。这些方法通过评估不同节点数量下模型的拟合效果和复杂性，帮助您找到一个平衡点，既能捕捉数据中的非线性关系，又能避免过拟合。

以上准则可能太过复杂，对临床医生很难理解，我们简化一点，给出两个方案：

直接选4（推荐），如果样本量少于50个，选3

选"根据最小AIC值自动计算"，系统会用3-7个分别建模，然后自动选AIC最小的模型

设置参照点

参照值（Reference Value）在限制性立方样条（RCS）方法中起到重要作用，它是作为自变量的基准值，用于比较和解释模型中其他自变量值的效果。选择一个合适的参照值对于模型的解释和理解具有重要意义。

参照值的定义：参照值通常是自变量取值范围内的一个特定点，模型结果将根据这个参照值来解释。例如，在研究年龄与某种疾病之间的关系时，可以选择一个年龄作为参照值，然后分析不同年龄段相对于这个参照值的风险比。

选择原理：在选择参照值时，有以下几个原则可以参考：

代表性：参照值应具有一定的代表性，通常应在自变量的分布范围内。选取分布较为集中的值作为参照值，可以使解释更加直观。

易于理解：参照值应该是容易理解的，以便于研究者和读者对模型结果进行解释。例如，在研究年龄与疾病风险的关系时，选择整数年龄作为参照值（如40岁、50岁等）会比选择小数年龄（如43.5岁）更容易理解。

实际意义：参照值应具有实际意义，与研究问题紧密相关。例如，在研究体重指数（BMI）与疾病风险的关系时，可以选择标准体重范围的中值作为参照值，这样可以更好地反映不同BMI水平下的风险差异。

以上解释比较繁琐，临床医生有时候难以消化理解，我们做了简化：

在本APP中，我们提供了两种常用的参照值选择方法：P10 和 Median。P10 指的是自变量分布的第10百分位数，表示10%的数据点低于该值。Median 则是自变量分布的中位数，即50%的数据点低于该值。这两种选择方法都具有一定的代表性和实际意义，可以根据您的研究需求和数据特点进行选择。

请大家任意选择，不影响结果！

选择图形风格

有多种图形外观和配色可以选择，都符合SCI杂志的要求。

在第一步中，生成的图形标出的点，是您选的参照点，并不是曲线的拐点，我们为了寻找曲线的拐点，还要进行第二步。

第二步：根据上一步生成的曲线，选择其形状和趋势，进行拐点分析

这一步主要目的是根据曲线的形状寻找拐点，如∪型曲线的拐点为最低点；∩型曲线的拐点为最高点；直线则无需探究拐点；而趋势没有逆转但斜率有变化的曲线，如指数/对数/阶梯/L型 曲线，则采用斜率变化的曲线切点。

判断很简单，肉眼观察，

如果看起来是一条直线，那么可以到此为止，线性关系的话，可以直接用传统的回归分析了，不需要RCS；

如果曲线的最高点不在两端，而在中间，那么就是n型曲线，选择n型曲线，系统就会把曲线最高点设置为参照点，同时也是曲线拐点；

如果曲线的最低点不在两端，而在中间，那么就是U型曲线，选择n型曲线，系统就会把曲线最低点设置为参照点，同时也是曲线拐点；

如果曲线的最低点和最高点在曲线两端，但曲线中间明显有斜率变化的拐弯倾向，则把拐弯的切点设置为参照点，同时也是曲线拐点。

如图：U型曲线，最低点在中间，把最低点设为参照点，也即是拐点。下一步用拐点分割数据即可。

第三步：分段回归

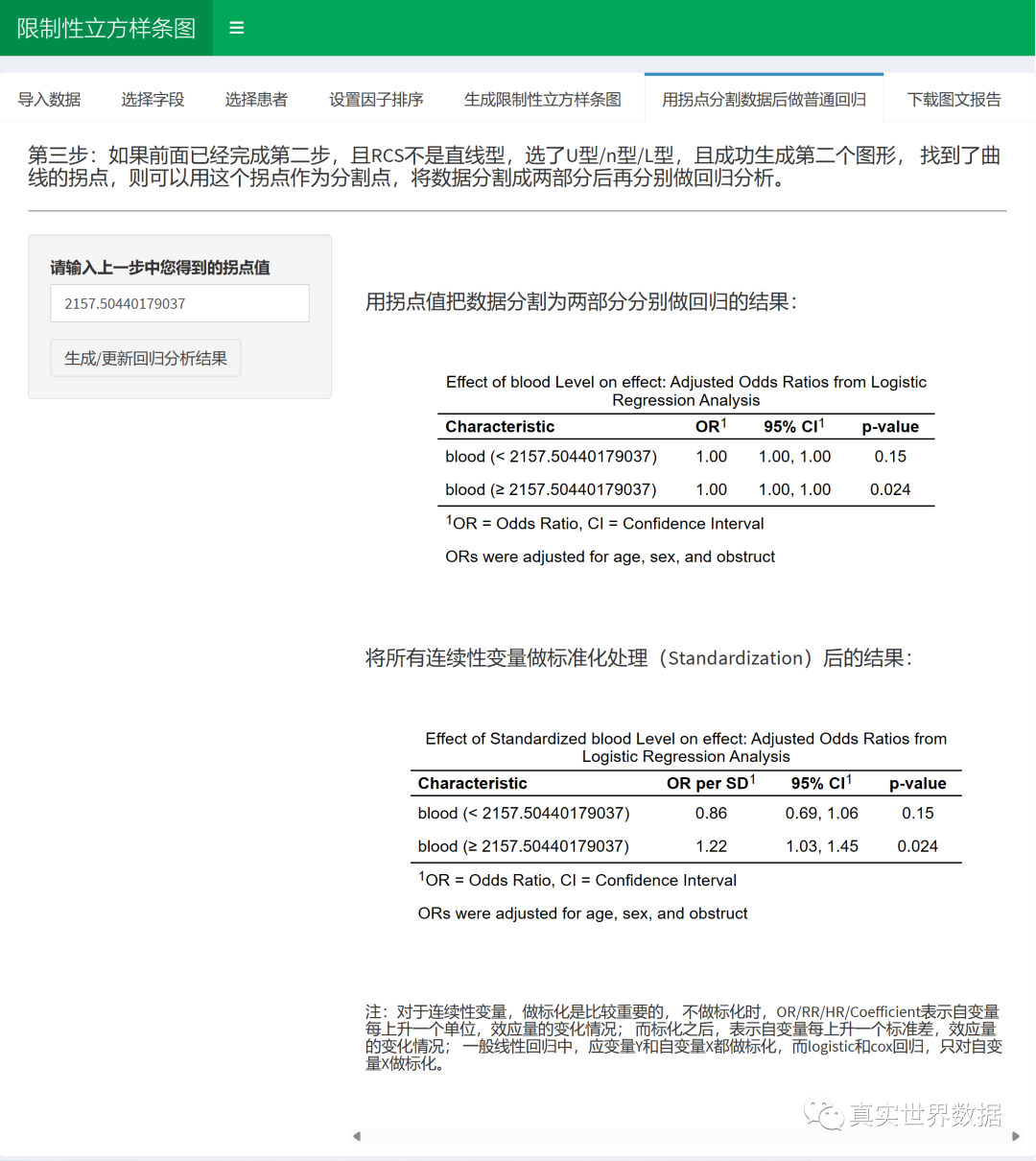
如果第二步找到了曲线拐点，则第三步用拐点分割数据，进行普通回归。当然，这部分也是自动一键完成的：

分割后，用两段数据分别做回归，但由于是连续性变量，OR值和1的差距很小，看不出大小，因此对于连续性变量，需要做标准化处理。

对连续性变量进行标准化（Standardization）是一种数据预处理方法，通过将原始数据转换为标准化后的数据，使其具有统一的度量尺度和比较基准。标准化的主要目的是消除不同变量间度量单位和数值范围的差异，便于在数据分析过程中进行比较和解释。

标准化的定义：对于连续性变量，标准化的过程通常是将每个数据点减去变量的均值，然后除以变量的标准差。标准化后的数据具有零均值和单位标准差，即：

标准化值 = (原始值 - 均值) / 标准差

标准化的意义：

消除度量单位差异：在多变量分析中，不同变量可能具有不同的度量单位和数值范围，如身高（厘米）、体重（千克）等。标准化可以消除这些差异，使得所有变量都具有相同的度量尺度，便于进行比较和分析。

提高模型稳定性：在某些模型（如线性回归、支持向量机等）中，标准化可以提高模型的稳定性和收敛速度，有助于获得更好的分析结果。

方便解释：标准化后的数据具有统一的比较基准，使得模型参数的解释更加直观。例如，在线性回归模型中，标准化后的回归系数可以直接反映自变量在相同标准差变化下对因变量的影响，便于进行解释和比较。

经过标准化处理之后，我们看到，拐点分割后的两部分数据，OR值是相反的，一个是小于1，保护因素，另一个是大于1，为风险因素。

这样的结果，如果是整体混在一起的数据，不做RCS是得不出来的。这就是RCS的作用。

下载word文件

最后，点击下载word报告，精心准备的图文就生成了，其中涉及到很多复杂的方法学描述，应该能给初学者提供很大的帮助：

当然，我们对结果的描述笔墨不太多，等拿到GPT-4的授权，就能自动生成论文。预计在2个月内，大家就能享受到自动生成论文的便利了。