 胡不归小故事
胡不归小故事从前有个少年外出求学,某天不幸得知老父亲病危的消息,便立即赶路回家.根据“两点之间线段最短”,虽然从他此刻位置A到家B之间是一片砂石地,但他义无反顾踏上归途,当赶到家时,老人刚咽了气,小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归?胡不归?…”(“胡”同“何”)
这个古老的传说,引起了人们的思索,小伙子能否提前到家?倘若可以,他应该选择一条怎样的路线呢?
这就是风靡千百年的“胡不归问题”——PA+k·PB型的线段最值问题。
早期的科学家曾为这则古老的传说中的小伙子设想了一条路线。(如下图)A是出发地,B是目的地;AC是一条驿道,而驿道靠目的地的一侧是沙地。为了急切回家,小伙子选择了直线路程AB。

但是,他忽略了在驿道上行走要比在砂土地带行走快的这一因素。如果他能选择一条合适的路线(尽管这条路线长一些,但是速度可以加快),是可以提前抵达家门的。
胡不归问题解答那么,这应该是哪条路线呢?显然,根据两种路面的状况和在其上行走的速度值,可以在AC上选定一点D,小伙子从A走到D,然后从D折往B,可望最早到达B。
那么,他应该如何选择回家的路线呢?

假设在驿道上行走的速度为,在沙地上行走的速度为(),在AC上选取一点D,设小伙从A到D的路程为AD,从D到B的路程为BD,则从A→B→D所有时间为
所以该题就转化为在AC上取一点D,使 值最小即可,这就是古老的胡不归模型
考试点“PA+k·PB”型的最值问题是近几年中考考查的热点更是难点。当k值为1时,即可转化为“PA+PB”之和最短问题,就可用我们常见的“将军饮马”模型来处理,即可以转化为轴对称问题来处理。
而当k取任意不为1的正数时,若再以常规的轴对称思想来解决问题,则无法进行,因此必须转换思路。
此类问题的处理通常以动点P所在图像的不同来分类,一般分为2类研究。即点P在直线上运动和点P在圆上运动。其中点P在直线上运动的类型称之为“胡不归”问题;点P在圆周上运动的类型称之为“阿氏圆”问题(参见阿氏圆模型)。
线段最值问题常用原理:
①三角形的三边关系:两边之和大于第三边,两边之差小于第三边;
②两点之间线段最短;
③连接直线外一点和直线上各点的所有线段中,垂线段最短;
胡不归模型例题1、如图所示,已知sin∠MBN=k,点P为角∠MBN其中边BM上的一个动点,点A在射线BM、BN的同侧,连接AP,则当“PA+k・PB”的值最小时,P点的位如何确定?

2、已知D为射线AB上一动点,∠BAC=30°,AC=,当AD=_____时,取最小值为_______.

3、如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则的最小值是_______.

4、如图,P为正方形ABCD对角线BD上一动点,若AB=2,则AP+BP+CP的最小值是_______.

5、如图,菱形ABCD的对角线AC上有一动点P,BC=6,∠ABC=150°,则线段AP+BP+PD的最小值为___.

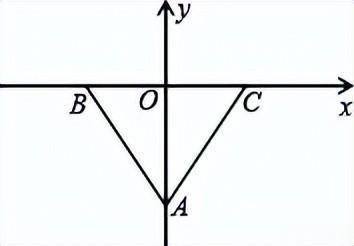
6、等边三角形ABC的边长为6,将其放置在如图所示的平面直角坐标系中,其中BC边在x轴上,BC边的高OA在Y轴上.一只电子虫从A出发,先沿y轴到达G点,再沿GC到达C点,已知电子虫在Y轴上运动的速度是在GC上运动速度的2倍,若电子虫走完全程的时间最短,则点G的坐标为_____________
7、如图,平行四边形ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD上的一动点,则的最小值等于_____.

8、如图1,在平面直角坐标系中,直线l与x轴、y轴分别交于点B(4,0)、C(0,3),点A为x轴负半轴上一点,AM⊥BC于点M交y轴于点N,满足4CN=5ON.已知抛物线经过点A. B. C.
(1)求抛物线的函数关系式;
(2)连接AC,点D在线段BC上方的抛物线上,连接DC、DB,若△BCD和△ABC面积满足,求点D的坐标;
(3)如图2,E为OB中点,设F为线段BC上一点(不含端点),连接EF.一动点P从E出发,沿线段EF以每秒1个单位的速度运动到F,再沿着线段FC以每秒53个单位的速度运动到C后停止。若点P在整个运动过程中用时最少,请直接写出最少时间和此时点F的坐标。

PS:例题解答私信:20230807
