第三节 基本矛盾粒子

一、矛盾粒子

表明在“粒子时空”里，27种对立粒子除光子外，是不稳定的，会通过三个正反简并律，简并叠加出八种非调和性的矛盾粒子，以及八种调和性的矛盾轻子。如正负电子、正反中微子等四种二重纠缠态的轻子。其量子数之和零守恒，穷尽了所有的可能，因而是完备的。

1、矛盾粒子的基本形态

1）辩证符号模型

2）矛盾粒子的组成构件

矛盾粒子是由矛盾结构配对子，以及矛盾结构配对子之间传递相互作用的简单矛盾关系子两个构件组成。

（1）矛盾结构配对子是由正反两种夸克配对组成，形成主次两方面的“两味四对”的矛盾结构配对子：

3）矛盾粒子的基本形态

在“两味四对”的矛盾结构配对子An1m1中间，依次分别与“两色四种”的简单矛盾关系子R1相结合，即可生成16种矛盾粒子。并依据矛盾粒子内部正反两方面之间的关系子的调和性，可将矛盾粒子分为非调和性的基本矛盾粒子和调和性的矛盾轻子两类形态。

（1）非调和性的矛盾粒子

在非调和性的基本矛盾粒子中，由于矛盾内部正反两方面之间只存在作用性的和反作用性的两种非调和性的简单矛盾关系子，由此可将非调和性的基本矛盾粒子分为作用性的和反作用性的两种形态。

不难看出，非调和性的矛盾粒子共有八种基本形态，并非全是自相矛盾的，而是把相容统一的形态，作为特例包含在内。而且最多只有八种形态，相互之间是独立的，穷尽了所有的可能，因而又是完备的。

（2）调和性的矛盾轻子

在调和性的矛盾粒子中，矛盾粒子内部正反夸克之间只存在作用反作用性的和反作用作用性的两种调和性的简单矛盾关系子，由此可将调和性的矛盾粒子分为左旋的和右旋的二重纠缠态。

在“两味四对”的矛盾结构配对子中间，依次分别与左右旋两种调和性的矛盾关系子相结合，可得八种调和性的矛盾粒子，亦为四种二重纠缠态的矛盾轻子，其粒子式分别为：

2、矛盾粒子的生成

1）矛盾粒子的简并生成

2）矛盾轻子的调和生成

八种矛盾轻子，也可由结构配对子两两相同的作用性的和反作用性的基本矛盾粒子在核聚变中调和生成，生成过程中伴有正反引力子或虚光子等释放。

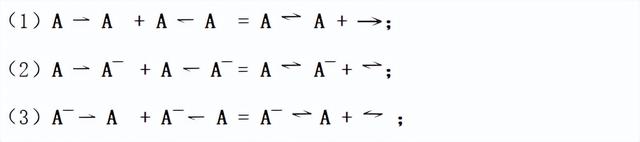
3）矛盾轻子的叠加生成

由式（4）和（8）可知，在左右旋电子中简并叠加有光子。这为电子因何能发射或吸收光子提供了理论依据。而正电子中却无光子叠加。说明在这种简并叠加情况下，正负电子是非对称性的，其对称破缺是由非对称性的简并叠加造成的。

3、矛盾粒子的量子“弦”表达和标识

八种非调和性的和八种调和型的矛盾粒子的粒子式，不仅难以区分且很难记忆。这就需要变换为量子弦象表达并“取名”，以便于区分和使用。依据矛盾粒子的结构子、关系子与正反量子弦之间的等同相变律：

八种非调和性的矛盾粒子，通过矛盾结构子、关系子与正反量子弦之间的等同相变律，就可等同相变为八个弦象。而且从左到右的粒子式，一一对应从上到下的量子弦象表达。参见表5—05。

2）调和性矛盾轻子的弦象表达

八种调和性的矛盾轻子，通过矛盾结构子、关系子与正反量子弦之间的等同相变律就可转化为三级调和四个弦象。而且从左到右的粒子式，一一对应从上到下的量子弦象表达。参见表5—06。

八种矛盾轻子亦为四种二重纠缠态的矛盾轻子，依次是正电子、中微子、反中微子和负电子等四种轻子。由此可见，调和性的矛盾轻子最多有四种，而且各自都是二重纠缠态的。这不仅与科学发现相符合，而且从理论上给出了其完备形态及其内部结构和生成方式。