下边的是圆柱体，我们都熟悉

圆柱体

圆柱体 是旋转体， 一个长方形绕自己的一条边旋转以后，就会形成圆柱体

下边这个是圆锥体，我们也熟悉

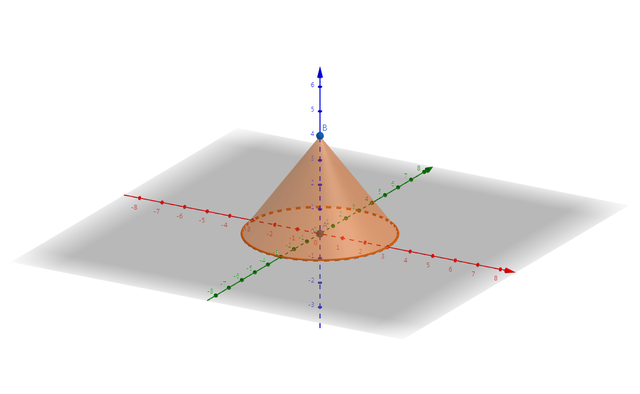
圆锥体

圆锥体也是旋转体， 一个直角三角形， 围绕自己的一条直角边旋转以后， 就会形成圆锥体

关于他们的 体积计算，我们也熟悉

圆柱体 的体积 等于 底面积 乘以 高

圆锥体的 体积等于 同底 等高 的 圆柱体 体积的 1/3, 就是 底面积 乘以 高， 再乘以 1/3

下边 这个立体，也是 个旋转体

抛物体

是由一个抛物线， y=x*x-3 围绕y 轴旋转形成的。

那这个 抛物体的 体积 该如何计算呢？ 它的体积 和 圆柱体的 体积公式，有简单的关系吗？

一个 连续函数 曲线 y=f(x) , x=a, x=b,以及 x 轴 形成的曲边梯形， 围绕 x 轴旋转以后， 形成的旋转体的体积， 可以按以下公式计算

旋转体体积公式

圆柱体的 体积等于 底面积 乘以 高

圆柱体的 底面圆 的半径 为 R 的话， 那 底面积 就等于 πR*R

上边 这个 公式里 也有 f(x) 的平方，再乘以π，

这样 算出来，就是 在 一个 特定的 x 点处，旋转体和垂直于 x 轴的平面， 形成的 截面圆 的 面积大小。

这样 把 旋转体 的 体积 看成， 由无数个 高为 dx, 底面积 为 π 乘以 f(x) 的平方， 的小薄圆柱 加起来的和， 一积分，就形成了 上边 这个公式。

下边就用微积分 计算一下 圆锥体的体积

这个直角三角形旋转后形成圆锥体

上边 这个图， 在 坐标面 上有一点 ， p(h, r)

将 这点 和 坐标原点O 连接起来，

这样， OP, x 轴， 直线X=h, 围成一个直角三角形，

这个直角三角形，围绕x 轴 旋转一个圆周以后， 就会形成 一个圆锥

圆锥的 底面 半径为 r, 高为 h

如果 按 旋转曲线看的话， 旋转的曲线 是 y=r/h *x, x的变化范围为 0 到 h

这样，直接 套公式，积分就可以， 如下图

积分计算圆锥体积

可以看出， 这样用微积分 计算出来的体积， 和用 立体几何公式 计算的结果是 一样的。

高中，立体几何 推导 圆锥体积公式，解释为什么 圆锥体积 是 同底等高圆柱 体积的 1/3 时， 拿棱锥做类比，因为 立方体，可以分割成 三个同底等高的 四棱锥，所以 每个四棱锥的体积就是 立方体的 1/3。 现在用 微积分 直接 积分，就可以推导出来了。