17世纪，艾萨克·牛顿提出了万有引力定律和运动定律，为理解天体运动奠定了基础。通过这些定律，二体问题（如地球绕太阳运动）得到了精确的解析解。然而，当引入第三个天体时，情况变得异常复杂。早期的数学家，如欧拉、拉格朗日和庞加莱，都尝试解决三体问题，但均未找到一般性的解析解。

基本假设

万有引力定律

任意两个质点之间的引力为：

其中：是万有引力常数。是质点和之间的距离。是从指向的单位向量。

运动方程

根据牛顿第二定律，质点 的运动方程为：

展开后，得到每个质点的加速度：

对于，需要分别写出三个这样的方程。

定义位置向量：设 是质点 的位置向量。

计算相互作用力

对于质点，受到质点 和 的引力：

类似地，对质点 和 写出对应的方程。

组成微分方程组

总共有 个质点，每个质点有 个坐标（在三维空间中），因此一共需要解决 个二阶微分方程。将二阶微分方程转换为一阶微分方程，可以得到一个 阶的一阶常微分方程组。

在三体问题中，我们研究三个质量分别为 的质点在万有引力作用下的运动。每个质点的位置和速度都是时间的函数。

下面我们具体推导将二阶微分方程转换为一阶微分方程的过程，并写出18个一阶常微分方程。

根据牛顿第二定律和万有引力定律，对于质点），其运动方程为：

简化后：

其中： 是质点 的位置矢量。 是质点 和 之间的距离。 是万有引力常数。

为了将二阶微分方程转换为一阶微分方程，我们引入速度矢量：

于是，对于每个质点，我们有

位置与速度的关系：

速度的变化率：

由于每个位置和速度矢量都有三个分量），因此对于三个质点，共有 个一阶微分方程。

进而得到质点 1 的微分方程

位置微分方程：

速度微分方程：

其中：

质点 2，3 的微分方程与质点1类似，这里省略。

汇总18个一阶常微分方程得到

位置微分方程（9个）

速度微分方程（9个）

其中距离的定义为

为方便计算和编程实现，我们可以将状态变量和微分方程表示为向量形式。

状态变量向量：

微分方程向量形式：

其中 是一个包含18个分量的向量函数，对应上述18个一阶微分方程。

为了求解上述微分方程组，我们需要给定初始条件，即在时间 时刻，各质点的位置和速度：

由于三体问题没有解析解，通常采用数值方法进行求解，例如：

下面是通过数值方法求解参数不同情况下三体运动轨迹的情况，可见其难以预测：

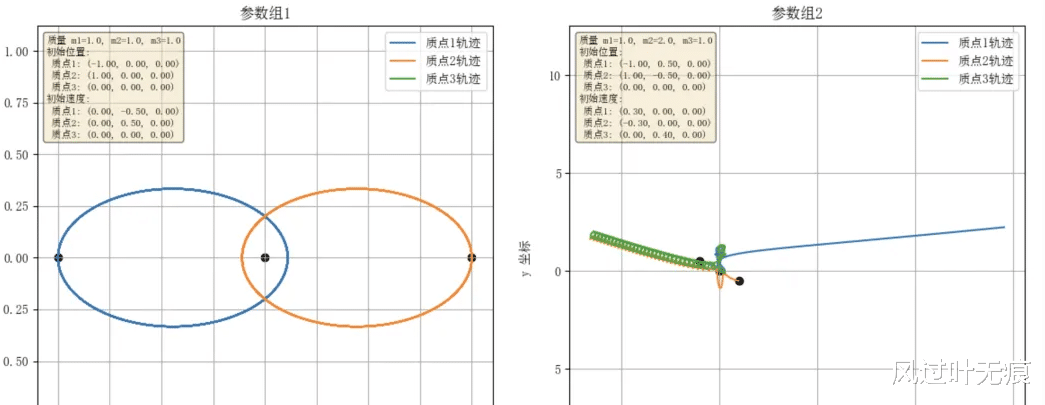
三体问题的数学模型揭示了在简单物理定律下，系统行为可以变得极其复杂。尽管我们无法找到一般性的解析解，但通过数值方法和对特殊情况的研究，人类对三体问题的理解不断深入。