
收集大家好奇的脑洞知识,整理有价值的学习资料,供一直奔波在学习路上的友友们参考借鉴
今年的国际圆周率日(3月14日),美国趣味科学网站报道称,总部位于美国加州的计算机存储公司“Solidigm”发布声明,该公司已将圆周率(π)计算到小数点后约105万亿位,打破此前1,00万亿位的世界纪录。

有人认为对圆周率的执着等同于秀肌肉,压根毫无意义。而事实上,科学家对圆周率的执着意义非凡,这背后隐藏着一个让人焦虑的奥秘。
了解π的定义和由来
π是一个数学常数,我们把它叫做圆周率,定义为圆的周长和其直径的比值。π是一个无理数,不能用分子表示,同时它还是一个超越数,不是任何有理数多项式的根。
早在大约公元265年,中国的数学家刘徽创立了割圆术,到了公元480年,通过割圆术计算出圆周率约3.1415926和3.1415927之间,到了现代的超级计算机,已经将圆周率计算到了100万亿位。
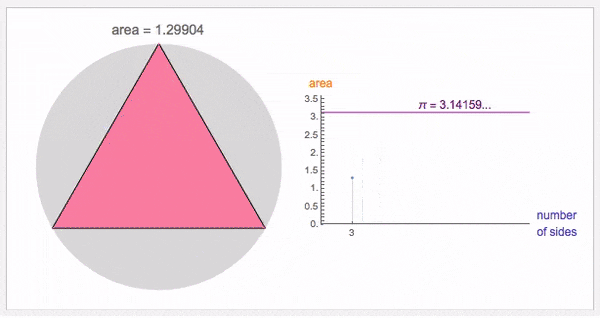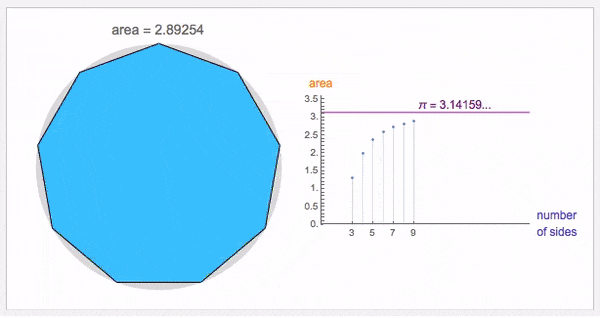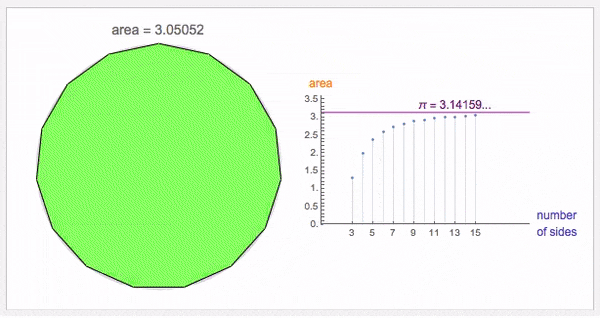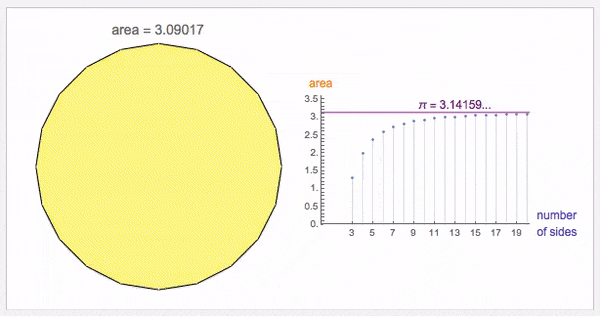
到了1706年,数学家威廉·琼斯在所出版的《新数学导论》中,提出用字母π表示圆周率,而这一符号真正被发扬光大是由数学家莱昂哈德·欧拉普及开来的。

试图把π算尽
在历史上曾有人执着的计算π,试图把π算尽,其中比较著名的是美国印第安纳圆周率法案。
据资料记载,1894年,印第安纳州一位业余的数学家爱德华·古德温坚信自己发现了化圆为方的正确解法,并强烈要求州参议员通过法律的形式确定这一真理,并授权给印第安纳州免费使用,不收取任何形式的专利使用费。

根据这位业余数学家的计算,得出了一个较为奇怪的结论:90度角的悬长和弧长之比为7:8,正方形对角线和一边之比为10:7, 直径与周长之比为5/4:4。因此π=8×4/10=3.2

漫画家Rock Island Argus所做的讽刺印第安纳圆周率法案的漫画
当时这份大胆又离谱的算法,辗转于金融委员会、沼泽地委员会等等部门。一位议员将该法案推荐给普渡大学的教授沃尔多指正,没想到,资深的沃尔沃教授直言道:自己见过很多疯子,所以不想见到更多。π有可能被算尽吗?
这一直是一下令人胆寒的议题,也是科学家执着于算尽的奥秘。
早在1947年,伊万·尼文就利用微积分和反证法证明π是无理数,如果未来被真实π能够被算尽,成为了一个有理数,那么这就意味着数学体系需要重新建立,而目前的科学测量标准将被统统推翻。

还记得上文提到的割圆术吗?
如果圆周率被算尽,割圆术就完全可以讲通了,根本就没有圆,而我们所理解的圆实际上等于正多边形,圆的光滑曲线实际上是无数个小线段。延伸来想,后思极恐!

1、曲线是不存在的。
我们会发现几何学中的图形会变得混乱不堪,相应的面积算法也彻底崩塌。

2、微积分是错误的
现代人利用微机分知识制成的集成电路将不再存在,航天工程中运用微积分制作的模拟轨道也不会出现,或者说出现的一切都是瞎蒙的。更为严重的是,物理中的很多常数都与π有关,因此组成物质的分子,原子的电子轨道可能会变得不稳定,物质能以凝聚成形,整个世界也会因此而受到牵连。

当然以上的设想都有点瞎操心,π目前已经被确定,无疑是一个无理数,也不可能被算尽的。因此科学家执着于计算它,还有另一个目的。
检验超级计算机能力
Solidigm公司能打破圆周率计算的世界纪录,绝不是轻而易举实现的,整整耗时75天,利用了100万的GB数据,需要的计算能力与数10万部智能手机相当。
可见计算圆周率的过程极其复杂,对计算机的运算能力和稳定性要求极高,因此,计算圆周率可以很好地辅助超级计算机的发展。

对于那些担忧“早晚有一天能将π算尽”的人来说,真的可以考虑去印第安纳州当议员。
▲我是姗姗,目标40岁退休的江南女子。关注我,就是在增长自己的知识点,提升自己的学习力!愿在这个混沌的世界里,遇见纯粹的你,坚持梦想的你,持续充电的你,共观这大千世界里的无限美景!

