石墨烯的理论强度推导基于以下核心假设:
1. 完美二维晶格假设假设材料为无缺陷单原子层结构,所有碳原子均以sp²杂化形成六边形蜂窝晶格(键长1.42 Å)。通过密度泛函理论(DFT)计算,其面内共价键强度达~130 GPa,而钢的典型键强度仅0.4-1.2 GPa。该模型忽略晶界、空位等缺陷对键断裂路径的影响。
2. 各向同性弹性假设在单轴拉伸下采用非线性弹性模型,其应力-应变关系满足:

其中为杨氏模量,为三阶非线性系数。该模型预测断裂应变为~20%,远超金属材料的典型值(钢约0.2%)。
3. 平面应力状态假设忽略厚度方向应力分量(因厚度仅0.335 nm),将断裂行为简化为二维平面内共价键的集体失效。实验测得单层石墨烯断裂强度为42 N/m,等效三维强度为130 GPa,是钢的200倍。
4. 断裂机制假设认为断裂由最大主应力控制,而非传统金属的位错滑移机制。石墨烯的sp²键断裂需克服约8 eV/Ų的势垒,而钢中铁原子键断裂势垒仅为0.5-1 eV/Ų。
二、理论模型与实验验证的对比参数理论值(完美晶体)实验测量值(含缺陷)差异机制解析杨氏模量1.05 TPa0.5-1.0 TPa基底约束、残余应变断裂强度130 GPa42 N/m(等效110 GPa)边缘缺陷主导断裂起始断裂应变25%10-20%局部应力集中效应热导率5300 W/mK4840-5300 W/mK声子边界散射增强注:实验值普遍低于理论极限,主要源于:
基底相互作用引入的残余应力(如SiO₂基底使有效模量降低~50%)
制备过程中产生的晶界、褶皱等缺陷(氧化石墨烯模量降至0.25 TPa)
断裂起始于边缘缺陷(通过AFM针尖诱导的裂纹扩展实验证实)
单层金属材料多轴应力失效模式的量化方法一、多轴应力状态的表征框架对于二维金属材料(如石墨烯、MXene),需建立以下量化模型:
1. 应力张量分解将三维应力张量投影到二维平面:
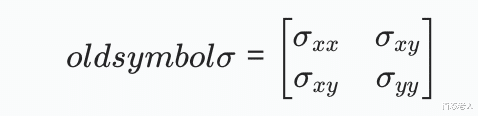
其中面内主应力可通过特征值求解。
2. 失效判据选择最大主应力准则:适用于脆性断裂主导的材料(如完美石墨烯):

实验测得石墨烯

von Mises准则修正:考虑二维塑性变形(如金属性MoS₂):

其中为二维屈服强度(MXene Ti₃C₂Tx约0.8-1.2 GPa)。
3. 屈曲失效分析在压缩-剪切复合应力下,屈曲临界应变由下式决定:

其中

为弯曲刚度,Lx,Ly为特征尺寸。
二、典型失效模式的实验与模拟数据材料应力组合类型失效模式临界应力/应变量化方法石墨烯双轴拉伸脆性断裂AFM纳米压痕实验MoS₂面内剪切+压缩层间滑移分子动力学模拟MXene拉伸-弯曲复合褶皱诱导裂纹扩展原位TEM观测金属碲化物循环多轴加载疲劳累积损伤Paris公式修正模型三、前沿量化技术进展1. 原位力学-电学耦合表征通过测量应变下电导率变化(如石墨烯载流子迁移率从$10^4 , \text{cm}^2/(V \cdot s)),反推晶格畸变程度。
2. 机器学习辅助多尺度建模采用深度神经网络预测缺陷敏感度:

其中为材料常数,ddefect为缺陷密度。
3. 微纳力学芯片技术集成MEMS传感器实时监测二维材料在多轴加载下的应变分布(空间分辨率达10 nm)。
总结与展望石墨烯的理论强度模型建立在完美二维晶格假设基础上,其与实验值的差异揭示了缺陷动力学的核心影响。对于多轴应力失效,需结合材料本征特性(如石墨烯的脆性与MXene的塑性)选择量化准则。未来发展方向包括:
开发适用于二维材料的统一失效判据(如引入拓扑不变量描述缺陷演化)
建立力学-电-热多场耦合实验平台(如同步辐射X射线衍射与Raman光谱联用)
探索极限尺寸效应(单层金属的理论强度极限验证,参见北京大学层裂实验进展)
通过跨尺度建模与高精度表征技术的结合,有望实现二维金属材料失效行为的精准预测与调控。
