量子力学,我们理解微观世界的基石,在解释和预测各种现象方面取得了惊人的成功。虽然标准的量子力学理论建立在复数域之上,但一个根本性的问题仍然存在:这种数学选择仅仅是一种方便的工具,还是自然本身必不可少的组成部分?
这个问题促使了对量子力学替代公式的理论研究,特别是那些采用超复数的公式。最近发表在《物理评论快报》上的一篇论文《复数与超复数量子理论的多路径和多粒子检验》深入探讨了这个问题,提出了新的实验方法,以严格检验复数在量子力学中的必要性,并探索超复数替代方案的潜在含义。
标准量子力学框架与复数的作用复数,即包含实部和虚部的数字,不仅仅是数学上的奇特概念,它们深深地融入了量子力学的结构之中。当我们考虑该理论的基本原理,特别是波函数、叠加和干涉时,它们的必要性就变得显而易见。
在量子力学中,粒子的状态由波函数描述,波函数是一个数学对象,它封装了关于粒子性质的所有信息。这些波函数本质上是复数值的,它对于描述诸如量子叠加之类的现象至关重要。在量子叠加中,粒子可以同时存在于多种状态。在数学上,叠加由波函数的线性组合表示,而复数对于捕捉这些叠加状态之间的相位关系至关重要。

此外,量子干涉现象是量子力学的一个标志,它在很大程度上依赖于波函数的复数性质。干涉源于波的叠加,而相对相位决定了干涉是相长干涉还是相消干涉。如果没有复数,量子实验中观察到的丰富的干涉图案,例如双缝实验,就无法得到充分的描述。量子力学的概率解释,即波函数模平方给出在特定状态下找到粒子的概率,也隐含地依赖于复数。
超越复数:探索超复数量子理论虽然复数为量子力学提供了卓越的服务,但数学家长期以来一直在探索复数的推广,即所谓的超复数。这些包括四元数和八元数,它们通过引入额外的虚数单位来扩展复数系统。例如,四元数有三个虚数单位(i、j、k),并且是非交换的,这意味着乘法顺序很重要。八元数则更陌生,它们既是非交换的,也是非结合的。
使用超复数构建量子力学的理论可能性一直是持续研究的主题。这种公式,称为超复数量子理论,可能带来新的物理学,并加深我们对量子力学基础的理解。复数和超复数量子理论之间的关键区别之一在于相位的性质。在标准的复数量子力学中,相位是可交换的,这意味着应用相移的顺序不会影响最终结果。然而,在超复数量子理论中,特别是那些基于四元数和八元数的理论中,相位可能变得非交换。相位的这种非交换性可能导致在精心设计的实验中观察到与标准量子力学的偏差。
多路径和多粒子检验的动机从历史上看,旨在探测复数在量子力学中必要性的实验测试一直受到限制。最突出的例子是佩雷斯检验(Peres test),该测试依赖于检查三路径干涉仪中的闭合相位关系,以寻找可能在超复数理论中出现的对标准复数量子力学的潜在违反。虽然佩雷斯检验提供了一些初步约束,但它主要关注单粒子干涉,并且在充分探索超复数量子理论的领域方面存在局限性。
论文《复数与超复数量子理论的多路径和多粒子检验》的出现,是为了弥补这些局限性。作者认为,为了严格检验超复数量子理论,并可能检测到相位非交换性的细微影响,实验需要变得更加复杂,涉及多路径和多粒子。这种向更复杂实验场景的转变,其动机是超复数理论中与标准量子力学的偏差可能在多路径和多粒子系统中变得更加明显,特别是由于这些理论中相位的非交换性质。
方法论:设计多路径和多粒子实验该论文提出了一种新颖的实验方法,以解决先前测试的局限性。它概述了多路径干涉测量和多粒子纠缠的理论框架和实验装置,专门设计用于对复数和超复数量子力学之间潜在的差异敏感。
在多路径干涉测量的背景下,该论文探讨了具有三个以上路径的干涉仪配置。通过增加路径的数量,干涉图案的复杂性增加,并且相位非交换性的细微影响(如果存在于超复数理论中)可能变得更容易检测。作者提出了可以隔离和放大这些潜在偏差的具体实验设计。
此外,该论文强调了多粒子纠缠在测试超复数量子力学中的重要性。纠缠是一种独特的量子现象,其中粒子以一种违背经典直觉的方式变得相关,是量子力学的关键方面。作者认为,通过研究多粒子的纠缠态,特别是在旨在探测相位关系的系统中,可以进一步提高对复数和超复数量子理论之间差异的敏感性。他们提出了涉及纠缠光子或其他量子粒子的实验方案,如果超复数量子力学确实是对自然界的正确描述,则可能会揭示超复数量子力学的特征。
预期结果和意义论文《复数与超复数量子理论的多路径和多粒子检验》主要是一项理论提案,概述了实验方向,而不是报告明确的实验结果。然而,它为未来的实验研究奠定了基础,这些研究可能对我们理解量子力学产生深远的影响。
这些提议的实验的主要预期结果是为复数在量子力学中的必要性提供更严格的检验。如果基于多路径干涉测量和多粒子纠缠的实验没有发现与标准复数量子力学预测的偏差,那么将进一步巩固复数作为自然界基本方面的作用。相反,如果实验结果揭示了与超复数量子理论预测相符的偏差,那将是一项革命性的发现,可能需要对我们对量子力学和物理学数学基础的理解进行重大修正。
这项研究的意义超越了量子力学数学结构的基本问题。探索超复数量子理论也可能对未来量子技术的发展产生影响。如果超复数量子力学在某些量子信息处理任务中具有优势,那么它可能会为量子计算、量子通信和量子传感开辟新的途径。此外,理解复数(或超复数)在量子力学中的基本作用可以更深入地了解量子现实的本质以及数学与物理世界之间的关系。




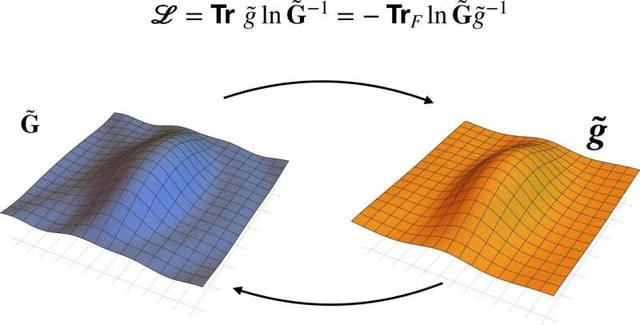

因果轮回是复数的体现[点赞][点赞]