“速度上限为光速”这一规则，对于大多数人来说，无疑是耳熟能详的。即便是那些没有深入学习过相对论的人，也可能曾在各种信息来源中零星地听到过这个概念，而且常常将光速与相对论联系在一起。也许是因为这样的普遍认知，许多人对突破光速限制的尝试产生了极大的兴趣。

下面是几种关于超光速的常见疑问举例：

①如果我边跑边用手电筒照，那不是意味着光的传播速度超越了光速吗？（超出了每秒30万公里的速度）

②假设有一根无限长的棍子，使其一端旋转，那么另一端的速度岂不是无穷大，从而超过光速吗？

③同样一根无限长的棍子，我在一端轻轻一推，另一端会立即发生移动，好像这样就可以瞬间传递信息，那不是说明信息的传递速度突破了光速的限制吗？

诸如此类的疑问不胜枚举，这里就不逐一列举了。

这些疑问通常都是在对相对论缺乏深入理解的前提下提出的，或者仅仅只是对某些理论条文有所了解，但并未进行数学推导验证，因此导致了这些疑问的产生。

实际上，对于这些问题的解答大致可以分为两类：

第一类：运用狭义相对论的几个基本推论（比如质量增加、速度叠加等）进行解释和反驳。

例如质量增加，站在观察者的角度，物体的速度越接近光速，其质量也会变得无穷大，进一步加速也就变得不可能（更严格的说法是，物体的能量变为虚数，下文将提及）。

第二类：告诉他们，现实中并不存在刚体，一根无限长的棍子在受力时会发生形变，传递这一形变的速度实际上就是固体中的声速，应力波传递信息，只有在刚体的情况下，才有可能超过光速。

但我们今天要讨论的，是光速无法被超越的一个更深层次的原因——因果律，这一解释并不常见，因为在多数情况下，上述几种解释已足够驳斥超光速的可能性。

然而，在上述几种解释中，有一个细节似乎被忽略了，那就是大部分关于超光速现象的物体都经历了一个加速过程，也就是说，这些物体的起始速度低于光速，通过加速来实现超光速。

但这种加速过程是有问题的，之前的解释已经告诉我们，由于需要无限多的能量来进一步加速，因此这种尝试是行不通的。（注：尽管这个解释看似合理，但关于物体质量增加这一点已经不再被采用，所以用能量的观点来解释，即质能方程，不涉及动质量，当物体的速度达到或超过光速时，其能量变得没有意义或成为虚数）

正是因为这样的讨论，导致我们一直将注意力集中在加速过程上，而很少去关注另一种情况——如果物体从一开始就以超光速运动会怎样呢？

正如光子从诞生就以光速运动一样，如果宇宙中存在一开始就以超过光速运动的物质，又该如何解释呢？实际上，针对这一点，上世纪有科学家提出了相关的理论——“快子理论”，假设存在天生速度超过光速的物质，即快子。而快子有其速度下限，不能低于光速（就像普通物质不能超过光速一样）。

然而，即便是不考虑加速过程，天生速度就超过光速的快子同样不能违背因果律。

接下来，我们来探讨今天的主题——因果律

因果律是一个非常古老的原则，称其为定律可能有些不习惯，因为因果律的内容可以说是基本常识，简单来说就是先有因后有果。在这个世界上，大概没有人会质疑这句话的正确性。

例如，在土壤中播下一颗苹果种子，经过一段时间后长出了苹果树。这个事件的顺序是先播种后长树，你能想象出先长树后播种的情况吗？

再比如，每个人都是先出生后死亡的，你能想象出一个人先死再生的情况吗？这就是因果律，违背因果律的事件是不能被接受的，这一点应该是毋庸置疑的。

那么，因果律是如何与超光速现象联系起来的呢？

在这里，我们需要先了解相对论中对事件的定义，一个事件指的是时空中的一个点（由一个空间点和一个时间点组成）。比如刚才提到的例子，播撒种子是一个事件（事件A），苹果树的长成是另一个事件（事件B），这两个事件构成了因果关系，并且事件B的发生时间必定晚于事件A，也就是说事件B的时间减去事件A的时间，结果必须大于零。

然而在狭义相对论中，时间不再是所有人都相同的物理量，不同参考系对同一事件的感知是不同的。例如，在你的参考系中，事件A发生在时间a，事件B发生在时间b，但在另一个人的参考系中，事件A还是发生在时间a，但事件B却发生在时间c。

由于因果律在所有参考系中都必须成立，结合前面的内容，将这些转换成数学表达就是：b-a＞0，c-a＞0，也就是说，只要这个数学公式成立，因果律就不会被破坏。

而这个数学公式和超光速又有什么关系呢？

接下来，我们简单介绍一下“世界线”的概念

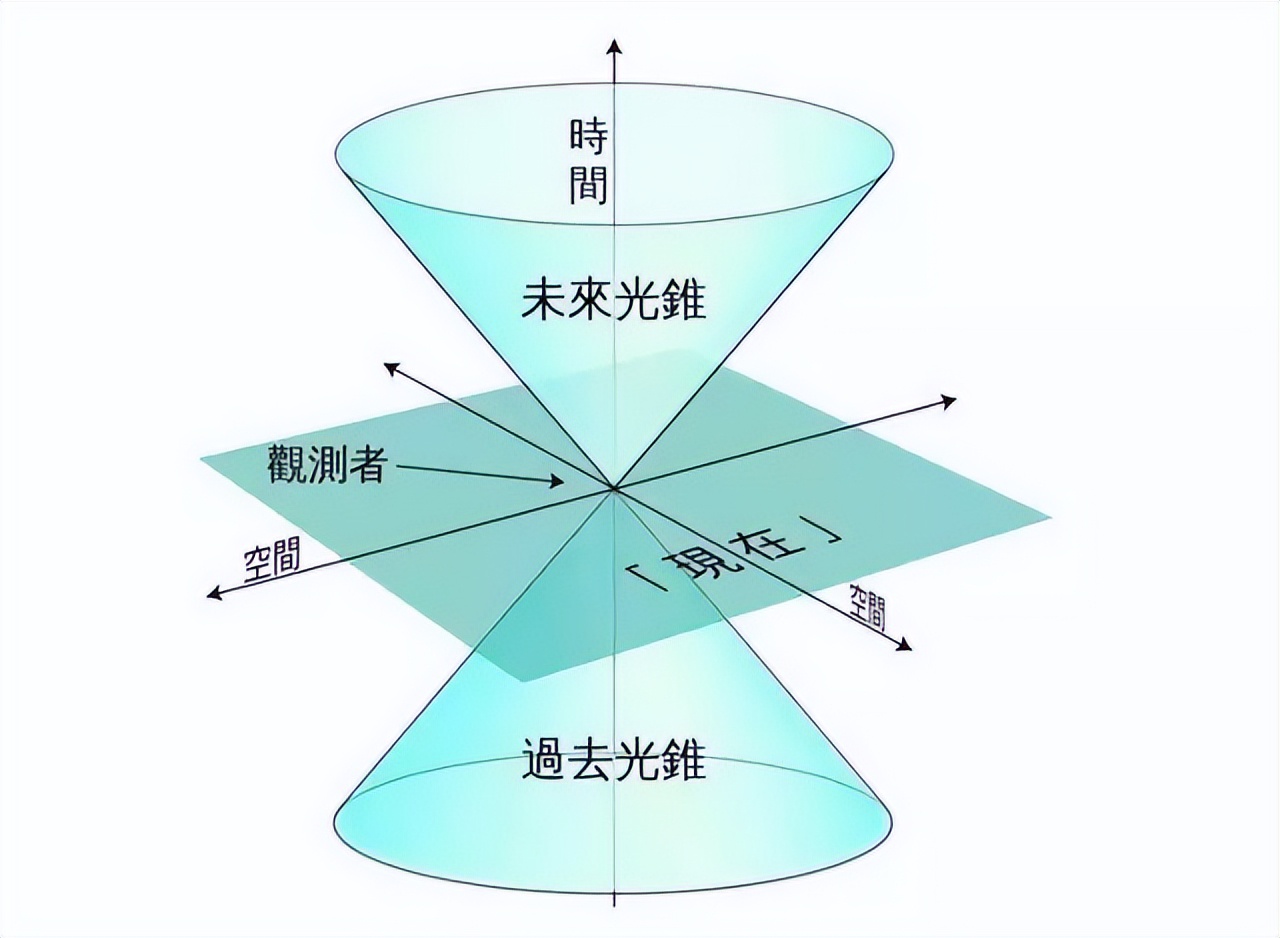
世界线是狭义相对论几何化后的概念，用几何语言描述相对论能更凸显其本质，世界线在这里被定义为一个物体自身事件的集合，如下图所示。

其中横轴代表空间，纵轴代表时间（我们称这个图为时空图），一个物体在每一时刻的空间位置都可以用一个时空点来表示，因此一条连续的曲线就构成了该物体的世界线。而物体的世界线分为三种：分别是类时曲线、类光曲线、类空曲线。

这三种世界线可以简单地描述为：类时曲线代表速度低于光速的物体的世界线，类光曲线代表速度等于光速物体的世界线，类空曲线代表速度超过光速物体的世界线，即超光速现象对应的是类空曲线。

在了解了这些之后，我们可以将问题归结为：类空曲线与数学公式b-a＞0，c-a＞0之间存在何种联系？

由于类空曲线与数学公式b-a＞0，c-a＞0都可以推导出同一个概念——时空间隔，那么时空间隔是什么呢？

简单来说，我们想象一下：在平面欧氏几何中，一个极短的线段长度是如何定义的？答案很简单，长度的平方等于（x²+y²）（其中x、y代表一端坐标轴上的极小长度，用微积分表示就是ds、dy），而在时空图中关于长度的定义与此类似（区别在于时间），被称为时空间隔。

回到问题，我们知道类空曲线的时空间隔是大于零的，而数学公式b-a＞0，c-a＞0可以通过洛伦兹变换转化为时空间隔，并证明其时空间隔是小于等于零的。

因此，我们可以得出结论：如果时空间隔小于等于零，则因果律成立；如果时空间隔大于零，则因果律不成立，判断的关键就是是否存在超光速。

另一个前提是我们坚信因果律在任何情况下都必须成立，因此超光速现象必须被排除！（也就是说，类空曲线不存在）

因此，超光速现象不存在的真正原因在于因果律不允许超光速的存在。