A*算法是一种高效的路径搜索算法，结合了Dijkstra算法的准确性（确保最短路径）和贪心最佳优先搜索的高效性。它通过启发式函数（Heuristic Function）动态调整搜索方向，适用于网格地图、游戏导航等场景。

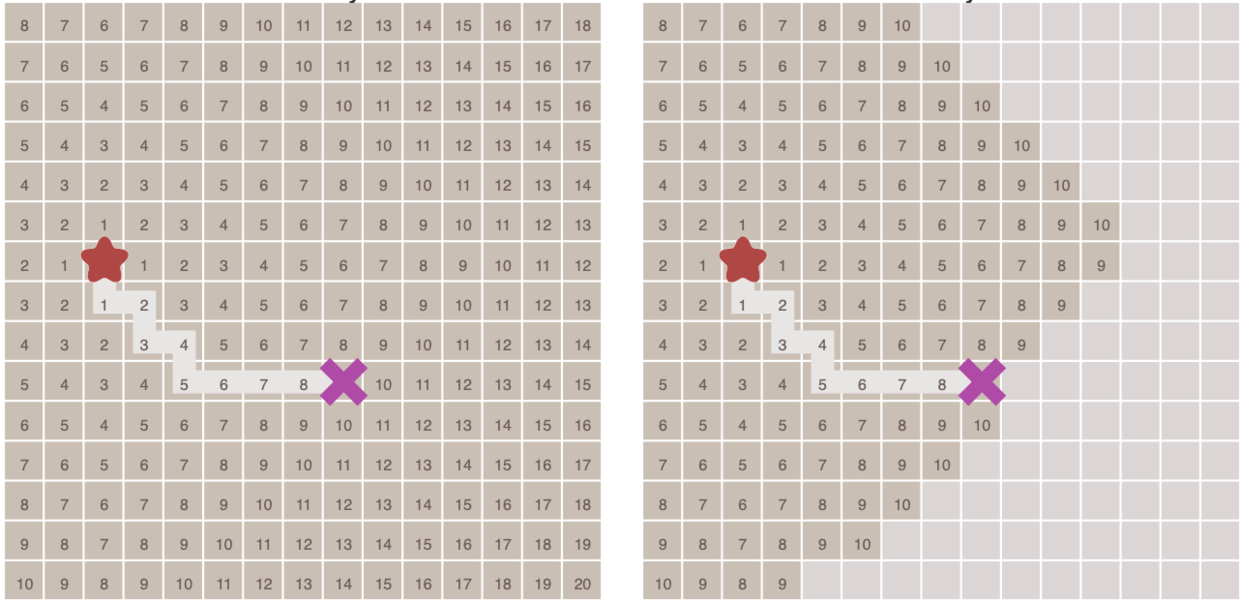
评估每个节点的优先级：[ f(n) = g(n) + h(n) ]- g(n)：从起点到节点n的实际代价。

- h(n)：从节点n到终点的预估代价（启发式函数，需可采纳，即不高估实际代价）。

初始化两个列表：

开放列表（Open List）：存储待探索节点（优先队列）。

关闭列表（Closed List）：存储已探索节点。

将起点加入开放列表。

循环直到找到终点或开放列表为空：

取出开放列表中f值最小的节点作为当前节点。

若当前节点为终点，结束循环并回溯路径。

遍历当前节点的相邻节点：

跳过障碍物或关闭列表中的节点。

若相邻节点不在开放列表，计算其g、h、f值并加入。

若已在开放列表且新路径更优（g更小），更新父节点及g、f值。

路径生成：从终点回溯父节点至起点。

曼哈顿距离（四方向移动）：[ h(n) = |x_1 - x_2| + |y_1 - y_2| ]

对角距离（八方向移动）：[ h(n) = (|x_1 - x_2|, |y_1 - y_2|) ]

欧几里得距离（任意方向，通常不可采纳）：[ h(n) =  ]

import heapqclass Node:    def __init__(self, parent=None, position=None):        self.parent = parent        self.position = position  # (x,y)        self.g = 0  # 实际代价        self.h = 0  # 启发式预估代价        self.f = 0  # f = g + h    def __eq__(self, other):        return self.position == other.position    def __lt__(self, other):        return self.f < other.fdef astar(maze, start, end):    # 初始化起点和终点节点    start_node = Node(None, start)    end_node = Node(None, end)    open_list = []    closed_list = []    heapq.heappush(open_list, (start_node.f, start_node))        # 四方向移动（上、下、左、右）    directions = [(0, 1), (0, -1), (-1, 0), (1, 0)]    while open_list:        current_f, current_node = heapq.heappop(open_list)        closed_list.append(current_node)        # 找到终点，回溯路径        if current_node == end_node:            path = []            while current_node:                path.append(current_node.position)                current_node = current_node.parent            return path[::-1]  # 反转路径        # 遍历相邻节点        children = []        for dx, dy in directions:            x = current_node.position[0] + dx            y = current_node.position[1] + dy            if not (0 <= x < len(maze) and 0 <= y < len(maze[0])):                continue  # 超出地图范围            if maze[x][y] == 1:                continue  # 障碍物            new_node = Node(current_node, (x, y))            children.append(new_node)        for child in children:            # 跳过已探索节点            if any(child == closed_child for closed_child in closed_list):                continue            # 计算g、h、f值            child.g = current_node.g + 1            child.h = abs(child.position[0] - end_node.position[0]) + \                      abs(child.position[1] - end_node.position[1])  # 曼哈顿距离            child.f = child.g + child.h            # 若节点已在开放列表且代价更高，跳过            if any(child.position == open_node.position and child.g >= open_node.g                  for (_, open_node) in open_list):                continue            heapq.heappush(open_list, (child.f, child))    return None  # 路径不存在# 示例地图（0可通过，1为障碍）maze = [    [0, 0, 0, 0, 0],    [0, 1, 1, 1, 0],    [0, 0, 0, 0, 0],    [1, 1, 1, 0, 1],    [0, 0, 0, 0, 0]]start = (0, 0)end = (4, 4)path = astar(maze, start, end)print("路径坐标：", path)

路径坐标： [(0, 0), (0, 1), (0, 2), (1, 2), (2, 2), (2, 3), (3, 3), (4, 3), (4, 4)]

优点：确保找到最短路径（启发式函数可采纳时），效率高于BFS和Dijkstra。

缺点：开放列表维护成本高，大地图可能消耗较多内存。

优化方向：二叉堆优化开放列表，跳点搜索（JPS）减少节点扩展。

通过灵活调整启发式函数，A*可适应不同场景需求，是路径规划领域的经典算法。