基本常数是我们理解物理宇宙的基石。这些常数包括光速 (c)、普朗克常数 (h) 和引力常数 (G) 等,它们是定义自然法则的参数。关于存在多少个基本常数的问题,让物理学家们困惑了数十年。在 George E. A. Matsas、Vicente Pleitez、Alberto Saa 和 Daniel A. T. Vanzella 的论文《从时空视角看基本常数的数量》中,提出了一种通过时空的视角来解决这一长期争论的新方法。
基本常数的概念深深嵌入物理学的结构中。从历史上看,这些常数被认为是描述宇宙中各种相互作用和现象所必需的。然而,完全描述物理世界所需的这些常数的数量是一个具有相当争议的问题。这场争论在 2002 年由 Duff、Okun 和 Veneziano 的文章中被显著地提出,他们对这一问题提出了不同的观点。Duff 认为基本常数的数量应为一,而 Okun 和 Veneziano 则提出了多个常数的观点。
基于时空的方法Matsas 和他的同事从一个全新的角度出发,通过聚焦于时空本身来研究这一问题。他们认为,通过将基本常数定义为用于构建时空的单位,可以导出一套最小的独立标准来表达所有受物理定律支配的可观测量。这种方法基于这样一个观点:时空的结构本质上决定了描述物理定律所需的基本常数。
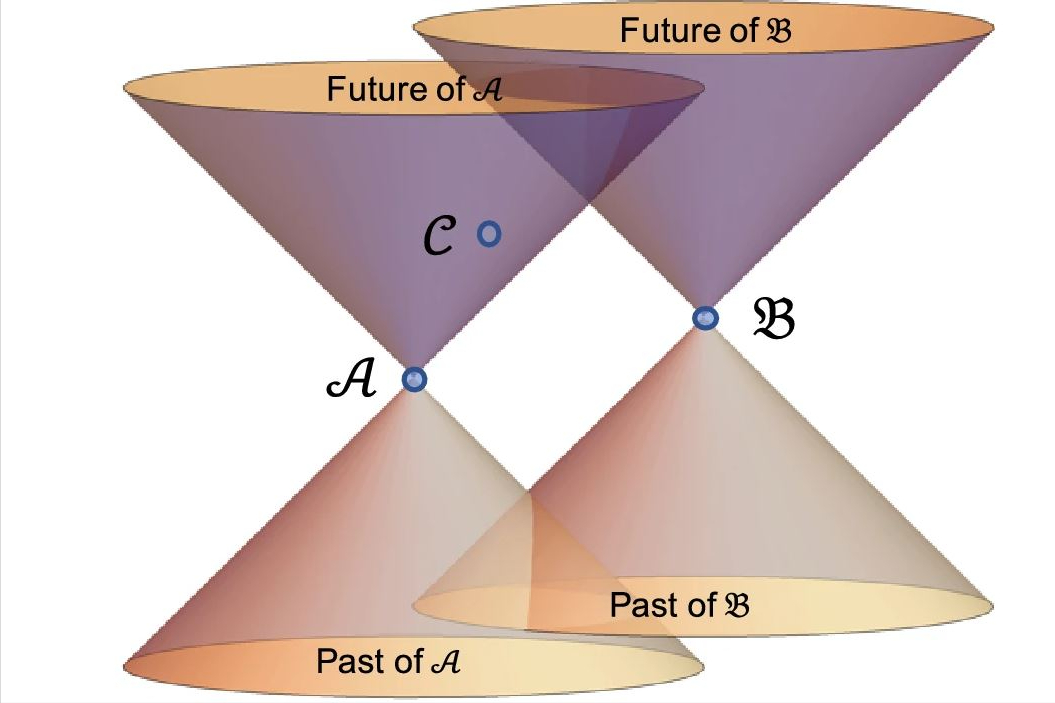
时空的作用在他们的分析中,Matsas 等人提出,用于测量时空的单位(如长度和时间)提供了定义基本常数的自然基础。由于所有物理现象都发生在时空的背景下,他们认为任何基本常数最终都必须用这些基本单位来表达。这导致了一个结论,即基本常数的数量与时空的性质密切相关。
一个基本常数Matsas 及其团队提出的核心论点是,在相对论时空中,所有物理量都可以简化为一个基本常数。这是一个深刻的结论,挑战了多个独立常数的传统观点。通过考虑时空的基本角色,他们断言一个常数足以描述所有物理定律,从而解决了 Duff、Okun 和 Veneziano 提出的争论。
含义和未来方向这一观点的影响是深远的。如果 Matsas 和他的同事是正确的,这意味着我们对宇宙的理解可以大大简化。这一统一可能带来新的见解和理论物理学的进展,提供一个更清晰和优雅的框架来理解宇宙。
然而,这篇论文只是一个开端。从时空结构中导出一个基本常数的概念需要进一步探索和验证。未来的研究需要检查这种方法在各种物理理论和实验数据中的适用性。此外,这一观点可能会开启探索时空本质及其与基本物理定律关系的新途径。
结论论文《从时空视角看基本常数的数量》提出了一种解决基本常数数量争论的引人入胜且创新的方法。通过时空的视角,Matsas 和他的同事提出一个常数足以描述所有物理定律。这一观点不仅挑战了传统观点,还为新的理论发展和更深刻地理解宇宙铺平了道路。随着研究的继续,这种基于时空的方法可能成为我们理解现实基本性质的重要一步。



