能量涣散值怎么计算的？

能不能理解为动能在介质里的传递过程呢？

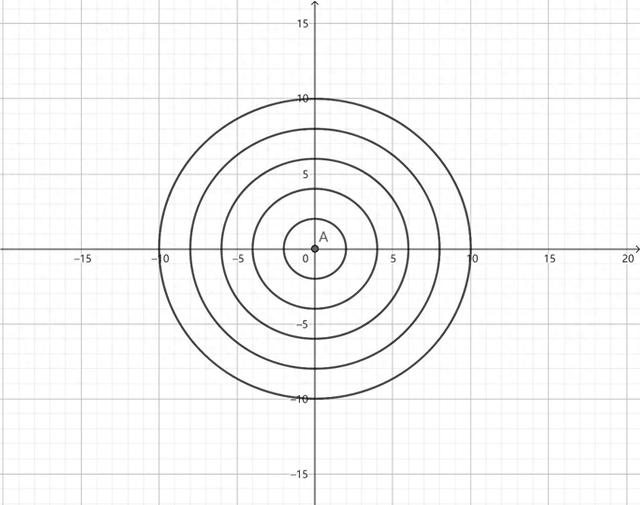
一个同心圆模型，看起来是二维的

把他做下圆心偏转，大脑感觉不那么平面了

再偏移，有点像深陷的旋涡效果

再偏移，好像来到了侧面，像龙卷风，又像旋涡隧道

所以把旋涡模型切片后，可以简单的看作一个个同心圆模型来计算

侧面看，同心圆像个喇叭，每个圈等距离划分，相当于上一个圆经过了一段时间后向外扩张的等比例值

那能不能假设，在同一个相同的介质里，比如水和空气的能量场，能量向外传递的速度都是等比例的同心圆扩张模型？

我们只要找出某一段横截面的圆心，就可以根据扩散时间和介质质量大小，计算出这股能量在这个时间段动能之间传递的能量大小

如图里公式，每个圆都是r²=x²+y²

都是同心圆，所以x²=0

那每个圆面积就是

r²=0+y²=y²

r²=y²

πr²=πy²

然后看侧面，定义t（f,g）为每两秒是一个同心圆的间隔

那圆（A,B）和圆（C,D）的关系是什么？

tr²π ，图里是按时间推移，面积增大

那（A,B）到（C,D）的面积，t（f,g）经过了0-2秒，（C,D）面积就是2r²π，r是（A,B）的初始半径

那把（A,B）看成一个球体动力源

y=f(x)，列出函数表达式

y=xr²π

球体（A,B）运动路径，动能会随时间推移，于自身半径平方向外传递动能

球体运动越快，动能传递的夹角越小，和速度成反比

时间t是个好用的变量，也可以理解为球体的位移距离s，按个人爱好理解就是

球体动能p=mv，质量m固定的，假设v固定一个值匀速运动

那动能p一样的情况下

介质密度看的就是同等时间t内（C,D）的面积大小

面积越大，动能传播的速度越快，介质密度越小

水的介质和空气的介质密度就能区分出来了吧？

那太阳系引力...

有没有介质传导动能呢？