过程奖励模型(PRMs)作为验证机制在提升大型语言模型(LLMs)性能方面展现出显著潜力。而当前PRMs框架面临三个核心技术挑战：过程监督和泛化能力受限、未充分利用LLM生成能力而仅依赖标量值预测，以及在测试时计算无法有效扩展。

针对上述局限，这篇论文提出了GenPRM，一种创新性的生成式过程奖励模型。该模型在评估每个推理步骤前，先执行显式的思维链(Chain-of-Thought, CoT)推理并实施代码验证，从而实现对推理过程的深度理解与评估。

下图直观地展示了GenPRM与传统基于分类方法的本质区别：

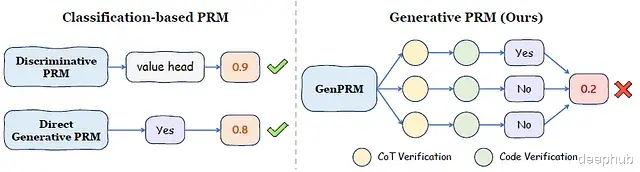
研究的主要技术贡献包括：

构建了一种生成式过程奖励模型架构，该架构通过显式CoT推理和代码验证机制，结合相对进展估计技术，实现了高精度PRM标签的获取

在ProcessBench及多种数学推理任务的实证评估表明，GenPRM在性能上显著优于现有的基于分类的PRMs方法

技术基础

1、马尔可夫决策过程框架

测试时扩展过程可形式化为马尔可夫决策过程(MDP)，定义为五元组(𝒮,𝒜, 𝑃, 𝑟, 𝛾)，其中：

𝒮表示状态空间

𝒜代表动作空间

𝑃定义转换动态

𝑟 : 𝒮 × 𝒜 → R为奖励函数

𝛾 ∈ [0, 1]是折扣因子

在此框架下，优化目标可分为两种：优化每个步骤的奖励(适用于基于搜索的方法)，或优化整体响应的累积奖励(适用于Best-of-N采样技术)。

2、监督微调技术

该技术训练模型基于先前上下文预测后续标记。针对数据集𝒟SFT = {(𝑥(𝑖), 𝑦(𝑖))}𝑁𝑖=1，监督微调损失函数定义为：

其中𝜋𝜃表示参数为𝜃的模型

3、测试时扩展方法

研究考察两种主要的测试时扩展技术：

多数投票机制：从所有可能解决方案中选择出现频率最高的答案

Best-of-N (BoN)采样：从N个候选解决方案中筛选性能最佳的答案

GenPRM架构设计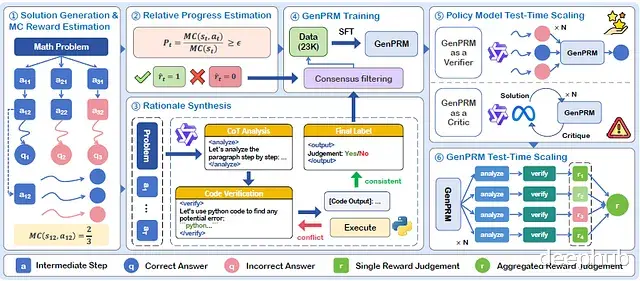

GenPRM框架由以下六个核心组件构成：

策略模型负责生成解决步骤，同时通过rollout轨迹估计蒙特卡洛(MC)分数

提出的相对进展估计(RPE)机制用于获取高精度PRM标签

通过增强的代码验证和CoT推理合成高质量过程监督数据

应用一致性过滤后进行监督微调(SFT)训练GenPRM

训练完成的GenPRM作为验证器或评论者，增强策略模型的测试时扩展能力

通过测试时扩展进一步提升GenPRM自身性能

从判别式PRM到生成式PRM的模型演进i) 现有PRM方法分析

a) 判别式PRM

假设存在PRM数据集𝒟Disc = {(𝑠𝑡, 𝑎𝑡), 𝑟𝑡}，其中硬估计PRM标签𝑟𝑡 ∈ {0, 1}。判别式PRM 𝑟𝜓通过交叉熵损失函数进行训练：

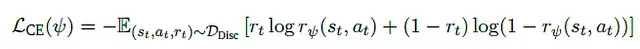
b) 直接生成式PRM

基于数据集𝒟Direct-Gen = {(𝑠𝑡, 𝑎𝑡), 𝑟𝑡}，其中正确步骤𝑟𝑡标记为Yes，错误步骤标记为No。直接生成式PRM通过SFT训练，为每个推理步骤预测Yes/No标签。对于步骤𝑡，将Yes标记的预测概率作为过程奖励ˆ𝑟𝑡：

ii) 生成式PRM创新设计

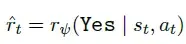
生成式PRM通过为直接生成式PRM增加类CoT显式推理过程实现性能提升。令𝑣1:𝑡−1表示从步骤1至𝑡−1的推理过程，𝑣𝑡表示步骤𝑡的推理。

基于数据集𝒟Gen = {(𝑠𝑡, 𝑎𝑡, 𝑣1:𝑡−1), (𝑣𝑡, 𝑟𝑡)}，GenPRM通过监督微调学习推理验证每个步骤。生成式过程奖励ˆ𝑟𝑡计算如下：

iii) 代码验证增强的生成式PRM

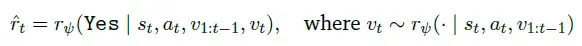
与标准生成式PRM不同，代码验证增强型GenPRM生成可执行代码验证推理步骤，通过代码执行结果提供客观判断。在步骤𝑡，生成推理𝑣𝑡(包含CoT分析和验证代码)后，执行代码并获取反馈𝑓𝑡。

给定当前状态𝑠𝑡、动作𝑎𝑡、先前推理序列𝑣1:𝑡−1及其对应执行反馈𝑓1:𝑡−1，PRM首先生成当前推理𝑣𝑡。执行代码并获取反馈𝑓𝑡后，最终的生成式过程奖励计算方式为：

GenPRM测试时扩展技术（TTS）i) 策略模型TTS：GenPRM验证器应用

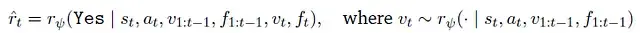
为扩展策略模型的测试时计算能力，可从策略模型采样多个响应，然后利用GenPRM作为验证器，通过并行TTS(Test-Time Scaling)方式选择最优答案。

ii) 策略模型TTS：GenPRM评论者机制

通过配备生成式过程监督能力，GenPRM可自然地作为评论模型优化策略模型输出，通过多轮顺序TTS方式扩展改进过程。

iii) GenPRM自身的TTS机制

在评估每个解决步骤时，系统首先采样N个推理验证路径，然后通过奖励平均值计算多数投票结果，得出最终预测。

对于不含代码验证的GenPRM，奖励计算公式为：

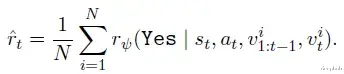
进一步整合代码验证和执行反馈的奖励计算公式：

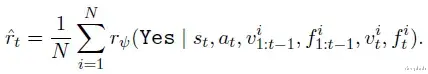
这些计算得到的奖励值可用于策略模型响应排序，或通过0.5阈值转换为二元标签，判定步骤正确性。

GenPRM数据合成方法

数据合成流程包含三个关键阶段：

i) 解决方案生成与蒙特卡洛估计

a) 步骤强制解决方案生成技术

利用MATH数据集训练集中的7.5K问题作为基础问题集

采用Qwen2.5–7B-Instruct作为生成模型，为每个问题收集多样化解决方案

具体实现中，添加"Step 1:"作为生成模型响应前缀，对于包含𝑇个推理步骤的完整响应，其标准化格式为：

步骤强制响应格式Step 1: {步骤详细内容}...Step T: {步骤详细内容}

为确保数据集包含足够的正确与错误路径样本，对难题和简单问题分别采样最多2048条解题路径，若采样2048个响应后仍未找到足够的正确或错误路径，则从数据集中剔除相应问题

b) MC估计精度与效率平衡策略

利用基于完成的采样方法估计各步骤正确概率

对于每个推理步骤𝑠𝑡，使用完成模型(特别是Qwen2.5-Math-7B-Instruct)生成𝐾个完成轨迹，并通过MC估计计算当前步骤𝑎𝑡的正确概率：

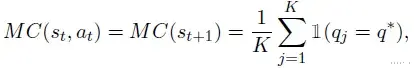
其中𝑞𝑗代表第𝑗个响应的答案，𝑞*为真实答案，1为指示函数

为平衡计算资源开销，根据估计的Pass@1 𝑀𝐶(𝑠1)动态调整𝐾值：

ii) 相对进展估计技术

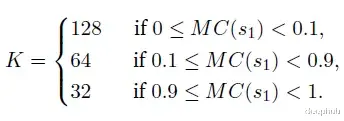
提出相对进展估计(RPE)方法，借鉴GRPO中相对优势估计思想，优化传统硬标签估计

MC分数作为当前状态𝑠𝑡的经验估计值。评估当前动作𝑎𝑡质量时，通过比较下一状态𝑠𝑡+1与当前状态𝑠𝑡的MC分数差异，其中𝑠𝑡+1 = [𝑠𝑡, 𝑎𝑡]

对每个响应，若第一个错误步骤为步骤𝑡′(即𝑀𝐶(𝑠𝑡′) = 0)，则将后续步骤MC分数设为0。步骤𝑡的RPE 𝑃𝑡定义为：

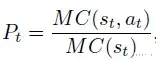
其中𝑀𝐶(𝑠1)为解决方案生成阶段计算的估计Pass@1值

通过引入阈值𝜖确定最终奖励标签ˆ𝑟𝑡：

iii) 推理生成、验证与过滤机制

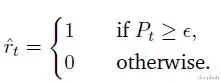
采用QwQ-32B作为推理生成模型，实现三步自动化管道生成并验证每个推理步骤

给定问题𝑥、真实答案𝑞*和候选步骤序列{𝑎1, · · · , 𝑎𝑇}，生成与验证流程如下：

步骤1：基于代码的推理生成

指导推理生成模型使用和标签封装CoT分析，使用和标签封装验证代码

采用以下结构化提示模板：（论文为英文prompt为了方便说明，我把它翻译成中文）

CoT和代码推理生成的提示模板[System]:你是一位数学老师。你的任务是使用python代码逐步审查和评论解决方案中的段落。[User]:以下是数学问题和解决方案（按段落分割，用标签封闭并从1开始索引）：[Math Problem]{problem}[Solution]<paragraph_1>{solution_section_1}</paragraph_1>...<paragraph_n>{solution_section_n}</paragraph_n>你的任务是验证解决方案中段落的正确性。按'### Paragraph {{ID}}'分割你的验证。你对每个段落的验证应由2部分构成，分别用'<analyze></analyze>'和'<verify></verify>'包装。1. 在'<analyze></analyze>'部分，你需要分析推理过程并详细解释为什么该段落是正确或不正确的。2. 在'<verify></verify>'部分，你必须以'''python\n{{CODE}}\n'''的形式编写**Python代码**来验证可以通过代码验证的每个细节。你可以导入PyPI（如'sympy'、'scipy'等）来实现复杂计算。确保在代码中打印评论结果。每段代码将由系统自动执行。你需要分析代码执行后的'[Code Output]'。>注意，编写代码时必须遵循'''python\n{{CODE}}\n'''的格式，否则代码将无法执行。完成所有验证后，如果你在某个段落中发现错误，返回**最早出现错误的段落索引**。否则，返回**索引-1（通常表示"未找到"）**。请将你的最终答案（即索引）放在$\boxed{{INDEX}}$形式的框内。

步骤2：代码执行与验证

执行生成的代码，获取步骤𝑡的反馈𝑓𝑡

执行反馈格式为[Code output: {execution result}]，作为前缀与生成的CoT分析和验证代码串联，用于后续处理

步骤3：标签判断与一致性过滤

完成所有候选步骤的推理数据生成与验证后，推理生成模型输出一个最终判断数字

若所有步骤被判断为正确，该数字为-1；否则，该数字表示首个错误步骤的索引

实验评估i) 实现细节

使用QwQ-32B模型和上述提示模板生成CoT分析与验证代码

基础模型选自DeepSeek-R1-Distill系列，包括1.5B、7B和32B三种参数规模变体

从生成结果中提取标签内容，重点关注策略模型预测为负面的步骤

ii) ProcessBench性能评估

下表展示了以F1分数衡量的ProcessBench评估结果：

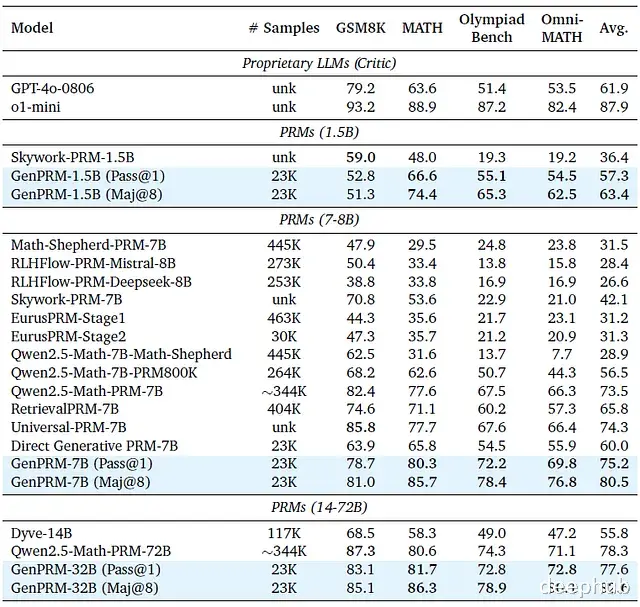
从表中数据可得出以下关键发现：

a) GenPRM在ProcessBench上性能优于基于分类的PRMs

GenPRM-7B显著优于直接生成式PRM方法，并在ProcessBench基准测试中超越了所有参数规模小于72B的现有PRMs模型。

b) GenPRM使较小参数规模模型通过TTS超越更大规模模型

GenPRM-1.5B通过简单的多数投票机制在ProcessBench上表现超过GPT-4，而GenPRM-7B甚至超越了Qwen2.5-Math-PRM-72B，这表明测试时计算扩展对GenPRM极为有效。

iii) 策略模型测试时扩展性能

a) GenPRM验证器模式评估

下图显示GenPRM-7B通过测试时扩展在性能上不仅优于同等参数规模的分类型PRMs，还超越了Qwen2.5-Math-PRM-72B：

图(a)-(d)展示了以Qwen2.5-Math-7B-Instruct作为生成模型时，GenPRM在MATH、AMC23、AIME24和Minerva Math四个数据集上的优势表现：

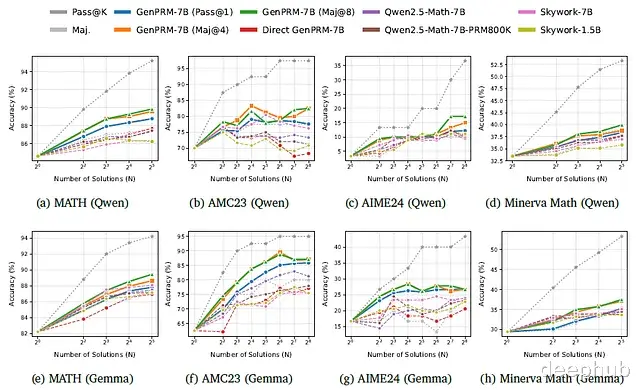
上图(e)-(h)进一步证明，GenPRM能良好泛化至以Gemma-3–12b-it作为生成模型的响应评估场景。

b) GenPRM评论者模式评估

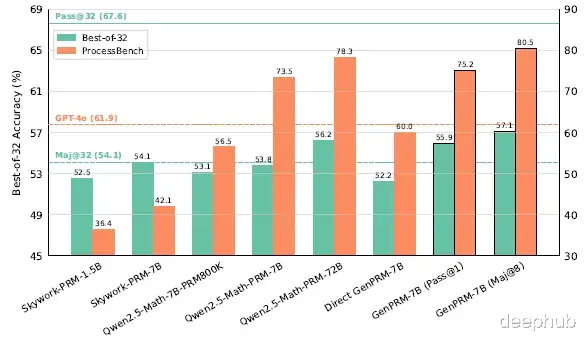
下表展示了批评改进实验的量化结果：

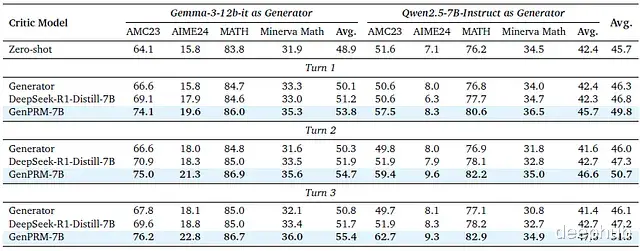
下图表明GenPRM比基线方法展现出更强的批评改进能力，能显著提升策略模型性能，且随着基于批评反馈的迭代优化次数增加，性能持续提升：

研究局限性

GenPRM通过生成式推理提供过程监督的方法在推理阶段引入了额外计算开销

当前研究主要关注数学推理任务领域，尚未全面探索在编码和通用推理任务上的实际应用效果

结论

研究提出了GenPRM，一种创新的生成式过程奖励模型，它通过执行显式推理和代码验证实现高质量过程监督，并使PRMs能够有效扩展测试时计算能力。在ProcessBench和多个数学数据集上的实验结果表明，GenPRM在性能上显著优于现有PRMs方法。研究还证实GenPRM的性能可通过测试时扩展技术进一步提升，且GenPRM作为评论模型具有很强的有效性。

https://avoid.overfit.cn/post/ef726bb5397a44f9832baff4668fb1e2