
“车轮悖论”,也被称为“同心圆悖论”,这是由古希腊哲学家、科学家和教育家亚里士多德在《论机械》(Mechanica)中提出的一个让许多数学家感到困惑的谜题:
假设有2个同心圆,一个是车轮,一个车轴,那么当车轮沿水平线滚动一圈时,这两个圆的底部会移动相同的距离,这究竟是为什么呢?
请看这个动图:

再来看一个:

发现问题了吧!
九年义务教育告诉我们半径R大的周长肯定比半径r小的周长颗肯定要长,那你怎么解释这两个圆却走出了同样的距离呢?
在刚性车轮的悖论中,四个同心圆看似都完成了一个旋转,它们沿着四条线段从左向右移动。
由于这些线段长度相等,人们自然会推测出所有圆的周长也应当相同,是吧?
然而,这个结论显然是不正确的,甚至一个蹒跚学步的孩子也能一眼看出问题。
那么,问题到底出在哪里呢?
这里有一个关键假设:刚性的车轮确实做了一个完整的转动。
为了更好地理解这一点,您不妨停下来,拿起笔和纸,亲自试一试。或者和孩子一起动手试试!当你准备好了,再继续往阅读。
回到主题。
在深入解决这个有趣的悖论之前,先让我们回到过去,了解一下亚里士多德之轮的起源。
其实,这个问题来源于亚里士多德的《力学》,这本著作包含了各种数学和哲学问题的简短集合,虽然不知道是不是当年大家一起写的,但为了给个著作权所以被传统上认为是亚里士多德的作品。

机械师: 右边的图是亚里士多德的车轮!
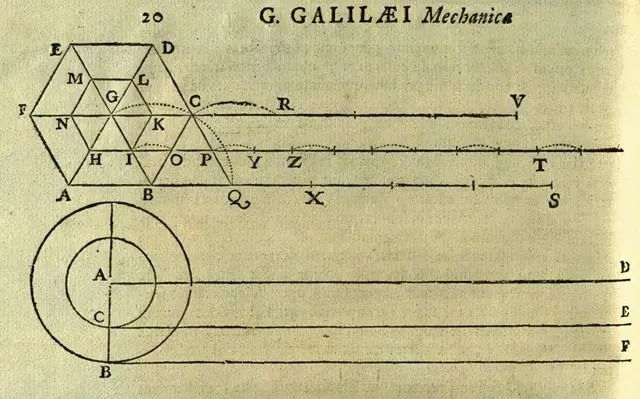
在《力学》中,"问题24" 提到了如下描述的车轮:
(注意下面这段话无需细看,了解即可!)
“让我们设想有一个较大的圆ΔZΓ和一个较小的圆EHB,它们的中心都在A点;设ZI是较大圆展开的直线,HK是较小圆展开的直线,且等于ZΛ。当我移动较小的圆时,我也同时移动它们的中心A,并让较大的圆与之连接。当AB垂直于HK时,同时AΓ也垂直于ZΛ,因此它们总是完成相等的距离,即HK对应于较小圆的周长HB,ZΛ对应于较大圆的周长ZΓ。如果四分之一圆展开的距离相等,那么显然整个圆展开的距离也会相等,因此当BH到达K时,周长ZΓ等于ZΛ,整个圆会被展开。以同样的方法,当我移动较大的圆并使较小的圆与之契合时,它们的中心相同,AB与AΓ同时垂直,后者垂直于ZI,前者垂直于HΘ。因此,当一个完成等于HΘ的直线时,另一个完成等于ZI的直线,ZA再次垂直于ZΛ,HA再次垂直于HK,因此它们将回到起始时的Θ和I状态。”
尽管这段话可能有些难以理解,但要点已经在开头提到了。
为了更直观地理解这个悖论,我们来看看两个模仿亚里士多德的车轮悖论木制拼图制作的动画。

动画来自网络
在第一个动画中,当内圈圆嵌在一个半径更大的外圈圆上,它从左向右滑动。请注意,当它移动时,尺子粗略地测量了两个整体之间的距离:从2厘米到6厘米。

动画来自网络
第二个动画,我们去掉大圆,只展示了滑动内圆。当它从左边移动到中心时,尺子粗略地描绘出了第一个动画中显示的相同距离(从2厘米到6厘米)。
奇怪不,那么,问题出在哪呢?

图中所示的车轮在从P1移动到P2的过程中进行了一个完整的旋转。那么,如何解决这个悖论呢?
伽利略对此进行了独创性的分析,他的方法如下:
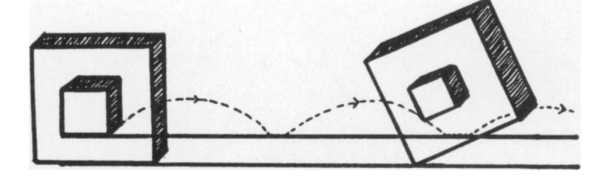
假设我们用两个正方形的轮子代替两个圆形的轮子。当大轮子在转角处旋转来完成四分之一的转动时,小轮子才会在转动时离开原来的位置。
所有这些小部分移动加起来,并给内轮额外的水平位移。
对于边数较多的多边形车轮,小车轮在旋转时执行许多较小的跳跃。同样,这些较小的跳跃达到顶点的内轮的额外位移沿轨道。

在圆形车轮的极限情况下,这相当于小车轮在转动时向前滑动。
在现代数学中,这个悖论的解答可以通过“滚动而不滑动”的概念来理解。

当两个圆相互接触且滚动时,它们的接触点在每个瞬间都有相同的线速度。
但是,因为外圆的周长比内圆大,所以内圆的每个点都必须滑动一些才能与外圆保持同步。
这意味着内圆的实际运动距离小于外圆,因此它们的周长并不相等。
亚里士多德的车轮悖论不仅在数学上引人入胜,也在哲学上引发了许多思考。
它挑战了我们对空间、运动和几何关系的直觉理解。这种悖论展示了我们的日常经验和数学理论之间的矛盾,使我们重新审视这些基本概念。
结语
亚里士多德的车轮悖论提醒我们,即使是看似简单的问题也可能包含深刻的复杂性。


看到悖论这词就想吐,所有的所谓悖论不过就是混淆概念罢了
没有悖论,要解释很简单,高速运动的汽车刹车,车轮止住不动,依然会留下十多米的刹车印记,车轮实际没有转动却走过了十几米的路程,文章里的小圆原理类似,只不过把长刹换成高频率的点刹
位移一样,而路程其实是不同的。大圆上的点路程更长
偷换概念而已
发光源在移动的时候,在运动前进方向上光的频率是会发生紫外频移的,在运动前进反方向上光的频率是会发生红外频移的,可以测速,即多普勒效应。现实中光速不是绝对的,请注意太阳系是运动的,银河系是运动的,在光速频移上就没体现出来,集体潜意识影响是巨大的。科研需要冲破集体潜意识。
很明显这个运动是滑动与滚动并存。同心圆旋转是角速度相同而不是线速度,上图所展开的同长度纯属扯皮。
刚性系统,里面的小圆不光滚动,还有滑动
和太阳系一样,除了转动,还有共同的平动而已。就算原地转动,你朝他们走过去,也会看到类似的场景
我在动车上踏步,从北京到广州,全是我自己走过去的[得瑟]
内圆不只是在滚动,同时在滑动
没有悖论,要解释很简单,相林的圆会给一个不为零的速度叠加。
轮与轴是固定的,轮一周自然轴也是一周,只是速度不同,这也是后来齿轮组的原理,变速箱是最常见的应用。
只有正确描述对比点的运行轨迹才能得到正确答案。
一个鸡蛋用心做是可以垂直立起,但遇到轻微的干扰力就会倒下,现在如果把鸡蛋内部的液体取出来,在鸡蛋壳内立起一个陀螺仪,陀螺仪的转轴两端和鸡蛋壳固定,如果在立起鸡蛋壳时,高速启动陀螺仪,在鸡蛋壳内部陀螺高速转动的时候,在鸡蛋壳顶部给一个水平向右侧干扰力,外表静止的鸡蛋壳会先向右侧倒下,紧接着已经又立起来,有时会颠倒立起来,完全违反角动量守恒,和牛顿第二定律。给鸡蛋壳内部装一个陀螺仪是有些困难,现在网上有卖带外部框架的陀螺仪玩具,完全可以代替完成本实验。按照经典理论可以用实践验证得到陀螺效应是违反角动量守恒,和牛顿第二定律的。为什么呢?深入研究得出时空的新发现,实验和理论结果已在整理中,准备在此公开奉献给大家。
没有悖论啊?!小圆的速度只是相对圆心而已,位移是需要相对地面的,可以想象一下圆心做的位移。初中物理就讲明白了。
把接触面积跟移动距离混淆
内圈圆除了滚动距离还有滑动距离
有点类似杠杠原理,半径越短周长利用率越高[doge]
车轮那是角速度
圆内部的圆不仅在活动还在滑动,悖论个毛线,纯属脑残
一个连滚带爬一个只滚不爬
瞎扯。最外圈转动,转轴带着圆心平动,两者之间位置当然是转动加平动
大圆拖着小圆[得瑟]
小编看来也不需要这么长的🦵,锯掉四分之三还省布料