行测题库|数量关系|每日一练:数学运算53

例题1
甲、乙、丙和丁四个依次相邻的农场分别饲养76头、82头、45头和93头牛,位置如下图所示(虚线位置为栅栏)。现由于两处栅栏损坏,有3个农场的牛混在一起。问最多需要分辨多少头牛,就一定能将所有牛还回原本的农场?
A.219
B.220
C.250
D.251
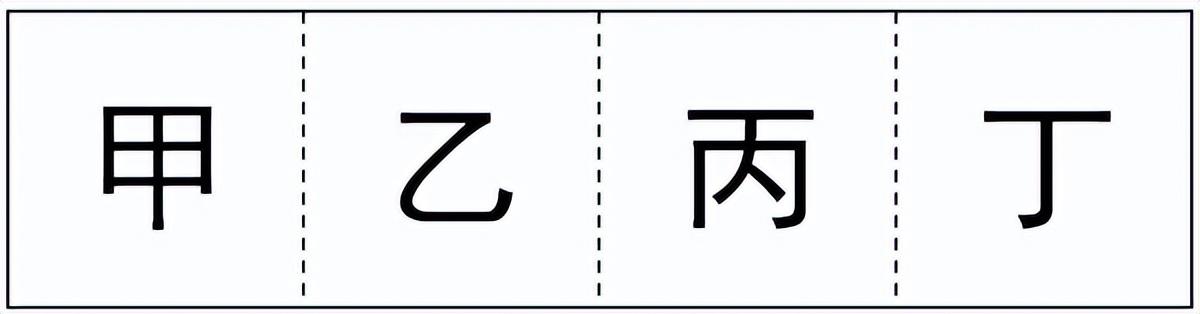
解析:
根据“两处栅栏损坏,有3个农场的牛混在一起”,可知有两种情况:①甲、乙、丙混在一起;②乙、丙、丁混在一起。
题目问最多需要分辨多少头牛,则混在一起的牛应尽可能多,由于甲(76头)<丁(93头),故应乙、丙、丁3个农场的牛混在一起,有82+45+93=220(头)牛。
因为还剩下最后一头牛时,其余两个农场已经分辨完毕,最后1头牛不需要分辨,故最多分辨219头。
因此,选择A选项。
例题2
农户张某今年年初将一块长方形农田扩建为正方形农田,使得正方形边长与长方形的长相同,今年的农作物产量是去年的1.5倍。已知今年农作物亩产量比去年高20%,则原来长方形农田的长是宽的多少倍?
A.1.2
B.1.25
C.1.5
D.1.6
解析:
设长方形的长为x,宽分别为y。则正方形的边长为x。
根据“今年农作物亩产量比去年高20%”,可赋值原来的亩产量为10,则现在的亩产量为10×20%+10=12。
根据“今年的农作物产量是去年的1.5倍”,“总产量=亩产量×面积”,可列方程:

解得x=1.25y。
因此,选择B选项。
知识点:
总产量=亩产量×面积。
例题3
某包装车间包装甲乙两种规格的袋装杂粮,甲乙两袋杂粮的重量之比为5:2,如果从甲袋中称出2公斤放入乙袋后,甲乙两袋杂粮的重量之比变为4:3。问甲袋杂粮原来重量为:
A.8公斤
B.10公斤
C.12公斤
D.15公斤
解析:
根据“甲乙两袋杂粮的重量之比为5:2”,可知:甲是5份,乙是2份;
根据“从甲袋出2公斤放入乙袋后,甲乙两袋杂粮的重量之比变为4:3”,可知:此时甲减少了1份,乙增加了1份,可知1份=2公斤。
甲原来是5×2=10(公斤)。
因此,选择B选项。
例题4
两个运输队,第一队有320人,第二队有280人,现因任务变动,要求第二队的人数是第一队人数的2倍,需从第一队抽调多少人到第二队?
A.80人
B.100人
C.120人
D.140人
解析:
设需从第一队抽调x人到第二队。
则第一队人数变为(320-x)人,第二队人数变为(280+x)人。
根据“第二队的人数是第一队人数的2倍”,可列方程:280+x=2(320-x),解得x=120。
因此,选择C选项。
例题5
一个袋子里红球、白球、蓝球的数量比例为3:8:4,再向袋子中放入14个红球和若干个蓝球后,红球、白球,蓝球的数量比例变为5:4:3。如果此时从袋子里取出10个红球、6个白球和2个蓝球后,袋子里剩余红球、白球、蓝球的数量比例为:
A.1:2:1
B.2:3:1
C.1:1:1
D.1:1:2
解析:
根据“红球、白球、蓝球的数量比例为3:8:4”,可设:刚开始时袋子里红球的数量为3x,白球的数量为8x,蓝球的数量为4x。
根据“再向袋子中放入14个红球和若干个蓝球”,可设加入 y个蓝球。则红球的数量变为3x+14,白球的数量变为8x,蓝球的数量变为4x+y。
根据“红球、白球,蓝球的数量比例变为5:4:3”,可列方程组:8x:(4x+y)=4:3①;(3x+14):8x=5:4②。
解得x=2,y=4。
此时袋子红球的数量为20,白球的数量变为16,蓝球的数量变为12。
根据“从袋子里取出10个红球、6个白球和2个蓝球”,可知:此时袋子红球的数量为10,白球的数量变为10,蓝球的数量变为10。即1:1:1。
因此,选择C选项。
