全文约1600字

大家好,我是古老师,专注于PMC(生产计划与控制)领域的教学。今天我们要介绍的是PMC系列中的第11个表格模型——累计求和表格模型。
累计求和模型通过计算一系列数值的累加总和来揭示数据的趋势和模式,广泛应用于销售分析、库存管理和生产控制等场景。它能够简化复杂的数据集,清晰地展示长期趋势,辅助决策制定,并提高对未来表现预测的准确性,从而支持PMC在编制生产计划时优化资源配置和战略规划。
累计求和是指从序列的第一个元素开始,依次将每个元素与其之前所有元素的总和相加,从而形成一个新的序列,其中每个元素代表原始序列中对应位置及其之前所有元素的累加值。公式如下:
 销售累计需求
销售累计需求接下来通过具体的案例来说明累计求和在PMC(生产计划与控制)工作中的具体应用。例如,在分析销售需求时,我们可以通过分析公司的产品销售趋势,判断销售额是否呈现明显的上升趋势。基于这些数据,可以进行更有效的资源分配和战略规划,如调整营销策略或优化库存管理。
假设A列为月份,B列为销售金额。为了计算累计销售金额,可以在C列的合适位置录入公式:
C2=SUM($B$2:B2)
然后将这个公式向下填充到相应的单元格中。然而,这种方法需要手动填充公式,容易出错。因此,建议使用动态数组公式来实现一键填充,减少错误的可能性。具体步骤如下:
D2=SCAN(0,B2:B13,SUM)

函数解释
SCAN:这是一个动态数组函数,用于遍历数组中的每个元素,并根据指定的累积逻辑生成一个新的数组。
0:初始值,表示累加的起始值。
B2:B13:要进行累加的数值范围,这里是从第2行到第13行的销售金额数据。
SUM:定义了一个匿名函数,对B2:B13的元素进行累计求和,相当于LAMBDA(a, b, a + b):定义了一个匿名函数,其中 a 是当前累加的结果,b 是当前处理的元素,a + b 表示将当前元素累加到现有结果上。。
这样,D列将会自动计算并显示每个月的累计销售金额,而不需要用户手动填充公式,减少了出错的可能性,并且更加高效。
库存最低方案累计求和还可以用于订单的排程规划。例如,某客户下达了一个订单:4500件(PCS)。此订单的前工序半成品生产是瓶颈,每天产能为300件,需要15天才能完成。而装配的产能为每天1000件。现在我们需要设计两种排程方案:
l 装配切换次数最少、效果最高的排程方案。
l 前工序半成品库存最低的方案。
假设B列为瓶颈日产数据,从B2到B16录入每日产能300件。然后在C列使用动态数组公式计算瓶颈的累计日产:
在C2单元格中输入以下公式:
=SCAN(0,B2:B16,SUM)
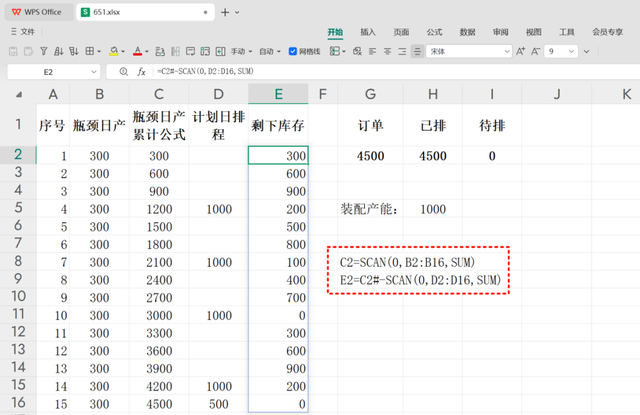
接下来,在D列分别在D5、D8、D10、D15、D16录入装配排程的数量:1000、1000、1000、1000、500。
为了判断剩余的半成品库存情况,在E列使用以下公式来计算剩余库存:
E2=C2#-SCAN(0,D2:D16,SUM)
其中,C2# 代表累计半成品瓶颈的日产结果数组。
通过这种方法,可以直观地展示每次装配排程后的剩余半成品库存情况,帮助实现最小化库存的目标,并确保不会超过设定的最大库存量(如1000件)。这样不仅优化了生产流程,还减少了库存积压的风险。
 切换最低方案
切换最低方案第二种方案是装配车间的零切换方案。由于此方案不需要装配车间工人来回切换生产线,生产效率将会得到提升。假设B列为瓶颈日产数据,从B2到B16录入每日产能300件。然后在D列的特定位置(D12、D13、D14、D15)录入装配排程的数量:1000、1080、1160、1260件。按照每日预计8%的效率提升目标进行排程,分别在第12、13、14、15天(D12:D16)进行连续排程:1000、1080、1160、1260件。
公式的设置与库存最低方案相同:
C2=SCAN(0,B2:B16,SUM)
E2=C2#-SCAN(0,D2:D16,SUM)

效果分析
通过上述公式和排程安排,可以发现:
此方案提高了装配效率,但半成品库存在第12天达到最高的3600件。
这表明虽然生产效率提升了,但由于集中排程导致了短期内较高的库存积压。
结论
PMC需要根据工厂的实际情况灵活选择库存优先还是效率优先的排程方案。如果工厂有足够的仓储空间并且希望最大化生产效率,可以选择零切换方案。反之,如果仓储空间有限且希望减少库存积压,则应考虑库存最低方案或其他折衷方案。
最终目的是找到最适合工厂当前运营条件的排程方案,以实现最优的生产效率和库存管理,达成工厂的整体运营目标。
