在牛顿的理论体系里，时间和空间是绝对且独立存在的，时间均匀地流逝，不受任何外界因素的干扰，空间则像一个永恒不变的框架，为万物的运动提供舞台。

然而，1905 年爱因斯坦提出的狭义相对论打破了这一传统认知。

狭义相对论建立在两个基本原理之上：狭义相对性原理和光速不变原理。

狭义相对性原理指出，所有惯性参考系对物理定律的要求是平等的，这意味着无论你处于何种惯性状态，物理规律都保持一致 ，比如在匀速行驶的列车上进行的物理实验，与在静止的实验室里所得结果并无二致；

光速不变原理则强调，在任何参考系下，真空中的光速始终是一个恒定的常数，大约为 299792458 米 / 秒，不会因为光源或观察者的运动状态而改变。

基于这两个原理，狭义相对论揭示了时间与空间的相对性。

比如说时间膨胀效应。当一个物体的运动速度接近光速时，其内部时间流逝的速度会相对于静止观察者变慢。

想象一下，有一对双胞胎，其中一人乘坐高速飞船进行星际旅行，另一人留在地球上。当飞船以接近光速的速度飞行一段时间后返回地球，会发现乘坐飞船的那个人比留在地球的双胞胎兄弟年轻许多，这便是时间膨胀效应的体现。

这种效应并非科幻作品中的虚构情节，而是经过了无数实验的验证。

例如，科学家通过将高精度原子钟放置在高速飞行的飞机上，与地面上的原子钟进行对比，发现飞机上的原子钟确实比地面上的走得慢，而且速度越快，时间变慢的效应就越明显。

时间膨胀效应可以通过一个简单而巧妙的方式推导出来，其核心涉及到勾股定理和洛伦兹因子。

假设有一艘飞船正在高速飞行，飞船内有一个光子钟，它由上下两面平行的镜子组成，光子在两面镜子之间来回反射，每反射一次就相当于 “滴答” 一声，记录下一个时间单位。

对于飞船内的观察者来说，光子的运动轨迹是垂直于镜子的直线，其往返一次的时间可以通过简单的距离除以速度来计算。设镜子之间的距离为 d，光子的速度为光速 c，那么在飞船内观察到的光子往返一次的时间 t' = 2d/c。

然而，对于飞船外静止的观察者而言，情况就有所不同了。

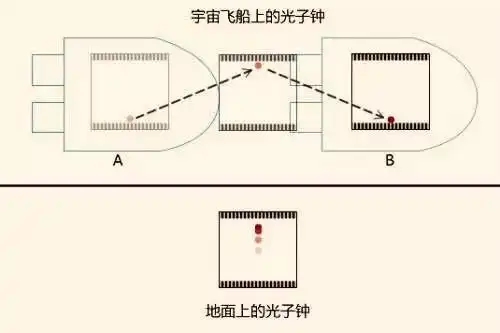
由于飞船在高速运动，光子在镜子之间往返的过程中，飞船也在向前移动。所以，在飞船外的观察者看来，光子的运动轨迹不再是垂直的直线，而是一条斜线，就像一个 “Λ” 形。

根据勾股定理，我们可以计算出这条斜线的长度。

设飞船的速度为 v，在时间 t 内，飞船向前移动的距离为 vt，光子在垂直方向上移动的距离仍然是 d，那么根据勾股定理，光子运动轨迹的斜线长度 d' = √((vt)² + d²)。因为光速不变，所以在飞船外的观察者看来，光子往返一次的时间 t = 2d'/c = 2√((vt)² + d²)/c。

通过对这两个时间表达式进行整理和推导，我们可以得到时间膨胀公式：t = t'/√(1 - v²/c²)。

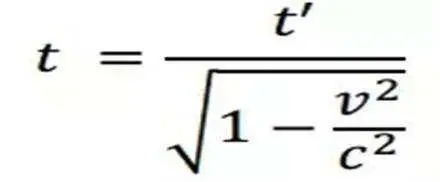
这里，1/√(1 - v²/c²) 就是著名的洛伦兹因子 γ，它反映了速度对时间流逝的影响程度。

当速度 v 无限接近光速 c 时，v²/c² 的值趋近于 1，那么 1 - v²/c² 趋近于 0，洛伦兹因子 γ = 1/√(1 - v²/c²) 就会趋近于无穷大。

这意味着，当飞船的速度无限接近光速时，飞船内的时间t'相对于飞船外的时间 t 会趋近于静止，即时间膨胀到了极致。例如，当飞船速度达到光速的 99% 时，洛伦兹因子约为 7.09，这意味着飞船内的时间流逝速度只有飞船外的约 1/7.09，时间被极大地拉长了。

这种时间膨胀效应是光速旅行中 “瞬间到达” 现象的关键所在，它让我们对宇宙中的时空有了全新的认识 。

当飞船的速度无限接近光速时，时间膨胀和尺缩效应这两种奇妙的现象会同时发挥作用，共同构建起 “瞬间到达” 的神奇体验。

时间膨胀效应使得飞船内的时间流逝速度大幅减缓，而尺缩效应则让飞船在运动方向上所感知到的空间距离急剧缩短，这两种效应相互交织，创造出了一种超乎想象的时空状态。

从时间膨胀的角度来看，随着飞船速度向光速逼近，洛伦兹因子 γ 急剧增大。

假设飞船以 0.9999c 的速度飞行，此时洛伦兹因子 γ 约为 70.71。这意味着飞船内的时间流逝速度仅为外界静止参考系时间流逝速度的 1/70.71。

例如，若外界静止参考系经历了 1 年的时间，飞船内的时间仅仅过去了大约 5.16 天。当飞船的速度更加接近光速，如达到 0.999999c 时，洛伦兹因子 γ 将约为 707.11，飞船内的时间流逝速度进一步减缓，外界 1 年的时间，飞船内仅过去约 17.3 小时。

与此同时，尺缩效应也在悄然改变着飞船所感知的空间尺度。

在飞船高速飞行的过程中，其运动方向上的空间距离会按照尺缩效应公式进行压缩。假设飞船要前往 1 光年之外的星球，当飞船以 0.9999c 的速度飞行时，在飞船内的乘客看来，这段 1 光年的距离会被压缩至约 0.014 光年。

这就好比原本漫长的星际旅程，在高速飞行的飞船内，被 “折叠” 成了一段近在咫尺的距离。如果将速度提升到 0.999999c，1 光年的距离在飞船内将被压缩至约 0.0014 光年，空间距离的压缩程度更加显著。

这种时间膨胀与尺缩效应的共同作用，使得飞船内的乘客在接近光速飞行时，仿佛进入了一个与外界截然不同的时空领域。他们所经历的时间变得极为缓慢，而外界的空间距离在他们眼中也大幅缩短，这就为无论多远都能 “瞬间到达” 提供了可能。

例如，当飞船以 0.9999c 的速度飞行时，对于外界观察者来说，飞船需要花费约 1.0001 年才能到达 1 光年外的星球，但对于飞船内的乘客而言，仅仅过去了约 1.7 天，这种巨大的时间和空间感知差异，充分展示了接近光速飞行时的奇妙时空特性。

光子的静止质量为零，这使得它从诞生的那一刻起就以光速在宇宙中飞驰。

根据狭义相对论，当物体达到光速时，时间膨胀效应达到极致，时间会完全停止。

对于光子来说，它在以光速运动的过程中，时间是凝固的，没有过去、现在和未来的概念。

从光子的视角来看，宇宙中的任意两点之间的距离都被压缩为零。

这是因为在光子的参考系中，空间的尺缩效应达到了极限。无论光子是从太阳出发到达地球，跨越约 1.5 亿公里的遥远距离，还是从宇宙的一端飞向另一端，在光子自身的 “感知” 中，都不需要花费任何时间，因为它所经历的时间是静止的，空间距离也为零，所以它可以瞬间到达宇宙中的任何位置。

这种光子视角的现象，与我们前面所讨论的接近光速飞行时的时间膨胀和尺缩效应是紧密相关的。当飞船的速度无限接近光速时，飞船内的时间流逝速度也会趋近于零，就如同光子的时间凝固一样；

同时，飞船所感知到的空间距离也会趋近于零，类似于光子眼中的空间状态。

这也就解释了为什么当物体的速度足够接近光速时，无论多远的距离，都能在某种意义上实现 “瞬间到达”，因为在接近光速的参考系中，时间和空间的特性发生了根本性的改变，使得遥远的距离变得不再遥远，漫长的时间也变得短暂到可以忽略不计。