数学，这门古老而神秘的学科，自古以来就以其独特的魅力吸引着无数的学者和爱好者。然而，数学的世界并非一片坦途，其中存在着许多令人望而生畏的难题，这些难题如同高不可攀的山峰，挑战着人类的智慧极限。今天，就让我们一同走进这些世界数学难题的世界，感受它们的神秘与魅力。

哥德巴赫猜想是数学家哥德巴赫于1742年提出的，它猜想任何一个大于2的偶数都可以表示为两个质数之和。尽管经过了数百年的研究，这一猜想至今仍未得到证明，也未被推翻，它如同一颗璀璨的明珠，吸引着无数数学家为之奋斗。

黎曼猜想是关于复分析中黎曼ζ函数的零点分布的猜想。它指出，黎曼ζ函数的所有非平凡零点都位于复平面上的临界线上。这一猜想对于数论的发展具有极其重要的意义，然而，尽管无数数学家为之努力，黎曼猜想至今仍然是一个未解之谜。

费马大定理是法国数学家费马在1637年提出的一个猜想，它指出当整数n>2时，关于x、y、z的方程x^n+y^n=z^n没有正整数解。这个看似简单的猜想，却困扰了数学家们300多年，直到1994年，英国数学家安德鲁·怀尔斯才最终证明了这一定理，为这一长达三个多世纪的数学难题画上了句号。

四色定理是一个著名的图论问题，它猜想任何平面地图都可以只用四种颜色来染色，使得相邻的区域颜色不同。这一猜想在1976年被美国数学家阿佩尔和哈肯借助计算机证明，然而，由于其证明过程复杂且依赖于计算机，这一证明在数学界仍然存在一定的争议。

庞加莱猜想是法国数学家庞加莱于1904年提出的一个拓扑学猜想，它指出任何一个单连通的三维闭流形都同胚于三维球面。这一猜想在2006年被俄罗斯数学家佩雷尔曼证明，他因此获得了菲尔兹奖，但他却拒绝了这一荣誉。

P vs NP问题是计算机科学中的一个核心问题，它探讨的是确定性多项式时间可解的问题（P类问题）与非确定性多项式时间可解的问题（NP类问题）之间的关系。这一问题至今仍未得到解决，它对于计算机科学的发展具有极其重要的意义。

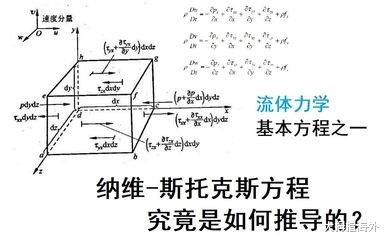
纳维-斯托克斯方程是流体力学中的一个基本方程，它描述了粘性不可压缩流体的运动。然而，这一方程的解的存在性与唯一性至今仍然是一个未解之谜，它对于理解流体的运动具有极其重要的意义。

贝赫和斯维讷通-戴尔猜想是关于椭圆曲线的有理点的猜想，它指出椭圆曲线的有理点的个数与椭圆曲线的某个算术不变量有关。这一猜想对于数论的发展具有极其重要的意义，然而，它至今仍未得到证明。

霍奇猜想是关于代数几何中的霍奇类的猜想，它指出代数簇上的霍奇类都是代数的。这一猜想对于代数几何的发展具有极其重要的意义，然而，它至今仍未得到证明。

阿贝尔群的分类问题是代数中的一个经典问题，它探讨的是如何对所有有限生成的阿贝尔群进行分类。尽管这一问题在一定程度上得到了解决，但其完整的分类仍然是一个未解之谜，它对于代数的发展具有极其重要的意义。

这些数学难题如同一座座高山，挑战着人类的智慧极限。尽管许多数学家为之奋斗，但这些难题至今仍未被完全攻克。它们的存在不仅推动了数学的发展，也激发了无数人对数学的热爱与追求。如果你对这些数学难题感兴趣，不妨深入研究，说不定你就是那个解开谜团的英雄！

PS：部分图文来自网路，侵删！