今天,我要带大家一起探索数学界的终极挑战——那些令人望而却步的未解之谜。这些谜题不仅考验着数学家的智慧,也为他们提供了获取百万美元奖金的机会。
2000年5月24日,美国克雷数学研究所(Clay Mathematics Institute,简称CMI)在巴黎举行了一次历史性的会议,提出七个被誉为““千禧年大奖难题”(Millennium Prize Problems)”的数学问题,并为每一个问题悬赏100万美元奖金。
而这这七个问题也代表了数学领域中最深奥、最具挑战性的谜团。
这七个问题分别是以下,我用通俗易懂的话描述了它们具体解决一个什么问题。
1️⃣ 黎曼猜想:找出素数的分布规律,是否遵循一个特定的数学函数的规律
2️⃣ P=NP问题:是否所有能快速验证答案的问题也能快速找到答案?
3️⃣ 霍奇猜想:复杂几何形状能否通过简单的数学方程完全描述?
4️⃣ 杨-米尔斯理论:描述粒子相互作用的理论是否总有稳定解?
5️⃣ Navier-Stokes方程组:流体流动的方程是否总是有光滑的解
6️⃣ 贝赫和斯维讷通-戴尔猜想:椭圆曲线的点数和L函数的关系
7️⃣ 庞加莱猜想:如果一个三维形状可变为一个球,那么它就是一个三维球(已被证明)
今天这篇我们重点聊聊黎曼猜想,篇幅原因,其他问题我们后面聊!

格里戈里·佩雷尔曼
而在这场智力挑战的22年后,我们发现,虽然这些问题仍然困扰着无数数学家,但其中仅有一个问题被破解,那就是著名的“庞加莱猜想”。
庞加莱猜想是由法国数学家亨利·庞加莱(Henri Poincaré)于1904年提出的一个难题。这个猜想关乎拓扑学中的一个基本问题。
简言之,如果一个三维形状能变形成一个球,那么它是不是一开始就是一个球?
经过了整整一个世纪的探索,2003年,俄罗斯数学家格里戈里·佩雷尔曼(Grigori Perelman)通过一种叫“黎曼几何流动”的方法,成功证明了这个猜想,帮助我们更好地理解三维空间的形状。
佩雷尔曼的解决方案不仅让他获得了全球数学界的赞誉,也让他成为了焦点人物。
然而,令人意外的是,尽管CMI向佩雷尔曼颁发了100万美元的奖金,他却选择了拒绝这笔奖金。佩雷尔曼的这一举动不仅引发了广泛的讨论,也让他在数学界的传奇故事更加丰满。
那么,除了庞加莱猜想之外的六个问题,为什么会被认为是如此的棘手呢?这些问题不仅涉及到复杂的数学理论,也在不断推动着数学研究的边界。
我们来看看👀。
1、黎曼猜想:猜想界的皇冠
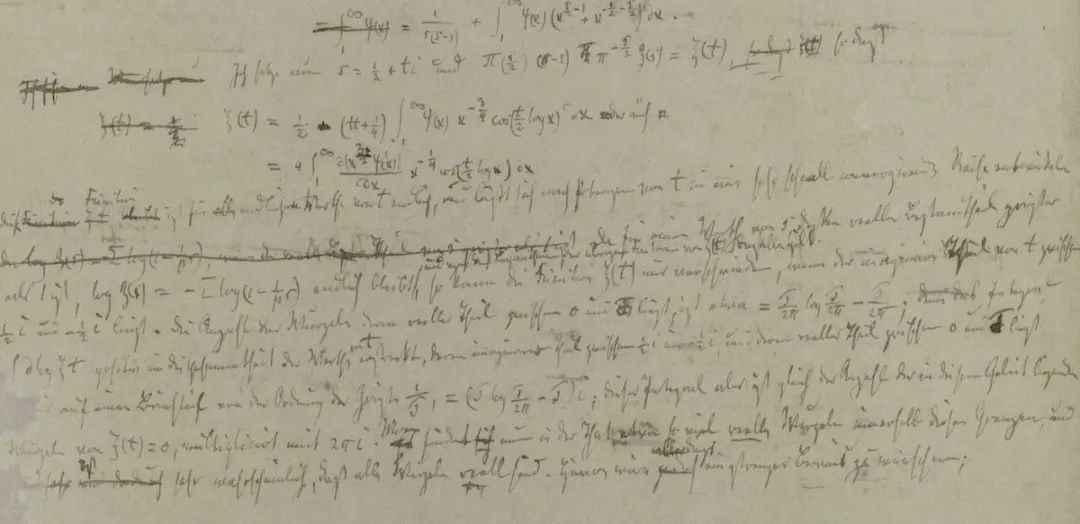
黎曼1859年,格丁根州立大学图书馆提供
黎曼猜想是由德国数学家波恩哈德·黎曼(Bernhard Riemann)于1859年提出的。
它涉及到对素数分布的深层次理解,是数论中的一个根本性问题。
素数,也称质数,也就是那些只能被1和它自己整除的数,比如2、3、5、7等等。素数在数学中有着非常重要的地位,但它们的分布规律一直是一个谜。
黎曼说:素数的分布是否遵循一个特定的数学函数的规律?这样理解应该清楚了吧。
所以说,这个猜想与素数的分布规律密切相关,至今仍未被证明。
即使是大数学家大卫·希尔伯特(David Hilbert)也曾感叹道:“如果我在沉睡了一千年后醒来,我的第一个问题将是:黎曼猜想被证明了吗?”
黎曼给出了一个ζ函数:
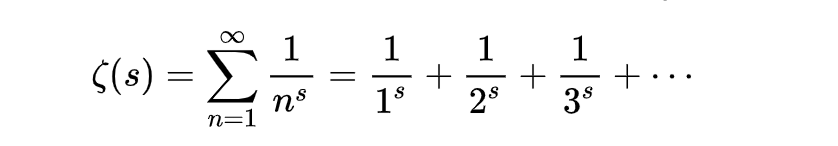
其中,s 是一个复数。当 s 为大于1的实数时,函数收敛,并且可以通过解析延拓将其扩展到复平面上的其他区域。
黎曼猜想的核心陈述是关于黎曼ζ函数的零点,也就是,除了位于(负)偶数的“平凡零点”之外,所有的“非平凡零点”都位于复平面上实部为1/2的直线上,即所谓的“临界线”上。
用数学语言来说,就是:所有非平凡零点 s 都满足:Re(s)= 1/2
这里的 Re(s) 表示复数 s 的实部。
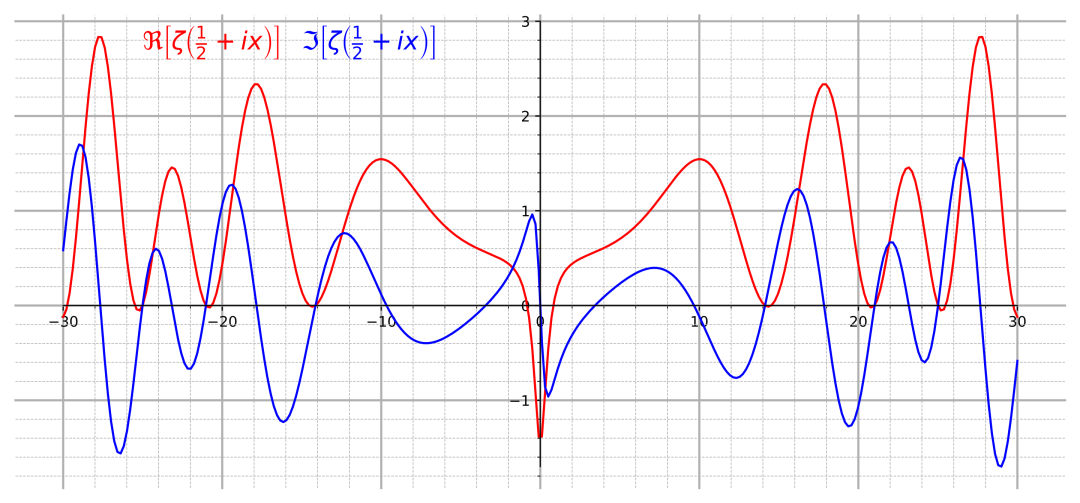
黎曼ζ函数在临界线上的线,如实(红线)和虚(蓝线)。可以看到最起初的几个非平凡零点就位于和上
有何意义呢?
想象一下,你在一个无限长的数轴上寻找素数。
素数就像随机分布在数轴上的闪亮星星,间隔时宽时窄。黎曼猜想就像是说,有一种神秘的地图(黎曼ζ函数),如果你能解读这张地图,就能预见下一颗闪亮星星(素数)的位置。

前1000个数字。每条黄线代表一个质数
你能证明吗?100万美金💲哦。
好,我们再看看剩下的问题,先一笔带过!
2、P=NP问题:计算复杂性的核心
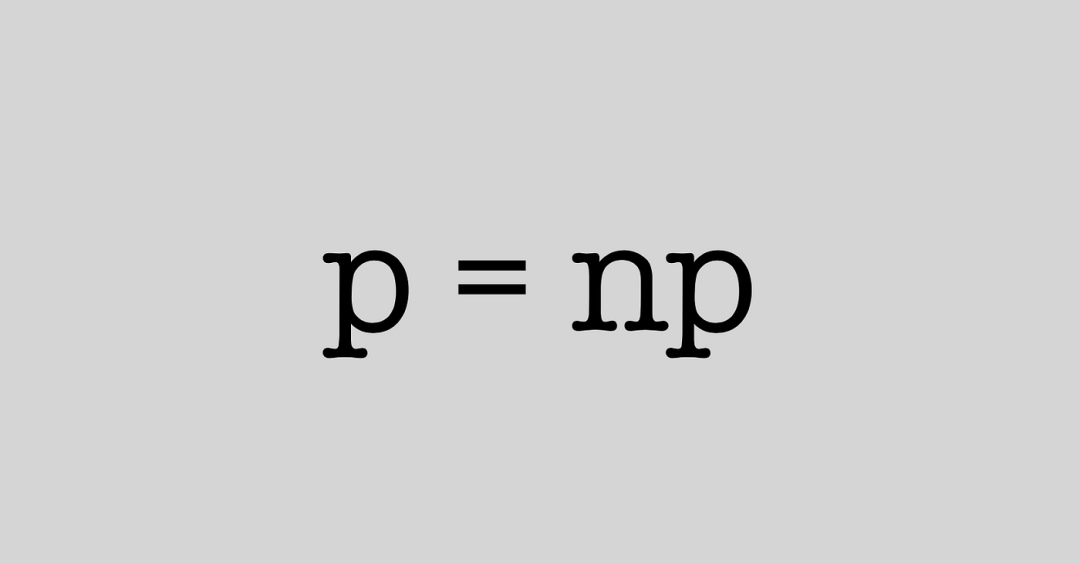
P=NP问题是计算机科学中的一个核心问题。
简单来说,它问的是“每一个可以在短时间内验证的解,是否都可以在短时间内找到?”
这是一个对算法设计和计算复杂性理论至关重要的问题,至今仍无定论。
在计算复杂性理论中,P和NP是两类不同的决策问题。
P(Polynomial time):指的是那些可以在多项式时间内由确定性图灵机解决的问题。简单来说,就是有一台理想的计算机,它可以在合理的时间内找到这些问题的解。
也就是说,如果你能在合理的时间内(比如几分钟)解开拼图题,那它就是一个P类问题。
NP(Nondeterministic Polynomial time):指的是那些可以在多项式时间内由非确定性图灵机验证的问题。这意味着,对于这些问题,如果给定一个候选解,我们可以在合理的时间内验证它是否正确。、
如果有人给你一个已经完成的拼图,你可以在合理的时间内验证它是对的,但你不一定能在同样的时间内自己解开这个拼图。
用数学语言来说,就是问P类问题是否等于NP类问题。
之所以P=NP问题的重要,主要在于它对许多实际问题有着直接影响。
如果P=NP,那么许多目前被认为非常困难的问题将变得可以在合理时间内解决。以下是几个领域可能受到影响的例子:
1-密码学:现代加密算法的安全性依赖于某些问题(如大整数分解、离散对数问题)在多项式时间内无法解决。如果P=NP,这些加密算法可能变得不再安全。
2-优化问题:许多现实世界中的优化问题,如物流、调度和网络设计等,如果P=NP,它们将可以高效地找到最优解。
3-人工智能:在AI领域,许多问题,如图像识别、自然语言处理等,都涉及到NP问题。如果P=NP,AI技术可能会取得重大突破。
3. 霍奇猜想:几何与代数的交汇
霍奇猜想是由英国数学家约瑟夫·霍奇(Joseph Hodge)于1950年提出的。
这个猜想涉及到代数几何和拓扑学的交汇,是理解几何对象的复杂结构和性质的重要理论基础。
4、杨-米尔斯理论:现代物理学的数学基础
杨-米尔斯理论是1954年由我国数学家杨振宁(Chen-Ning Yang)和米尔斯(Robert Mills)提出的。
它是现代物理学中的一个重要理论,为描述粒子物理中的基本交互作用提供了数学基础。
5、Navier-Stokes方程组:流体动力学的难题
Navier-Stokes方程组描述了流体在不同条件下的运动规律。虽然它在工程和物理学中有广泛的应用,但在数学上,这些方程是否总是有光滑解仍然是一个未解的难题。
6、贝赫和斯维讷通-戴尔猜想:群论中的未解之谜
贝赫和斯维讷通-戴尔猜想涉及到群论中的一个深奥问题,探讨了某些数学对象的结构性质。
虽然这些问题至今未解,但它们的存在激励着无数数学家和研究者继续前行。每一个难题不仅是对数学能力的挑战,更是对人类智慧的极限考验。
正如许多伟大的数学家曾经所言,数学不仅是解答问题的过程,更是探索未知世界的旅程。
总结:
我们总觉得自己越到的数学很难,但是和千禧问题比起来,不堪一击!
也许有人也会说,这些问题解决了能怎么样?
那我可以告诉你,如果费马大定理早几百年被证明的话,我们的科技说不定比这更先进呢!
