过滤趋势组件是总结时间序列数据的一种有用方法，因为它允许人们捕捉并关注真正重要的特征。但是过滤方法可能会导致信息丢失，因此是有代价的。然而，Linear State Space Models(LSSM)为提取观测变量的未观测趋势成分提供了一种实用的方法。

Local Linear Trend Model

插件实现了以下框架：

上述模型非常灵活，在实践中很难将未观察到的趋势值与实际水平区分开来。在这种情况下，将趋势方程的方差限制为零可能有助于获得平滑的随机趋势。也可以像Hodrick-Prescott滤波器那样，在一开始就施加一个外生的惩罚参数，控制趋势的平滑性。

通过信号方程中的回归量，可以向模型中添加任何类型的解释变量(s)或干预效应(s)。

应用于每周信用卡支出数据

由于多种原因，高频金融变量通常是有噪声的，其中大多数甚至在事实发生后无法控制或识别。过滤掉因市场状况周期性变化而自然产生的噪声成分，可以为我们提供一个清晰的潜在趋势图，而不会丢失太多关键信息。在本练习中，使用了土耳其每周信用卡支出数据（见Figure 1）。

信用卡支出数据在数值层面上看起来并不平滑，而当我们查看周变化时，它变得更加波动不定（见Figure 2）。

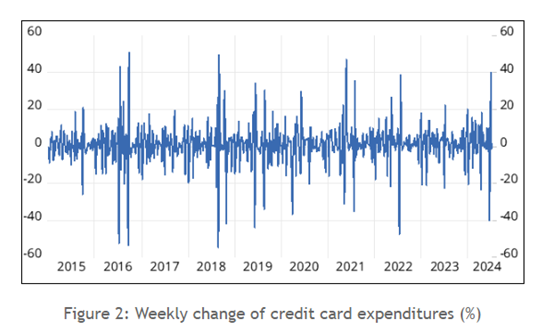
数据中频繁且剧烈的波动使得难以解读其潜在动态。随机趋势估计可能有助于过滤掉数据中的此类波动。

为了估计局部线性趋势模型，我们可以使用插件（见Figure 3）。

取对数有助于减轻此类标称变量中通常存在的规模效应。平滑随机趋势的估计也可能有助于进一步降低潜在分量中的噪声。最后，我们可能要考虑季节性，看看支出模式是否会随着日历月而变化（见Figure 4）。

在滤除噪声以及控制季节效应后，信用卡支出的动量损失变得更加明显。

References

Durbin, J. and Koopman, S. J. (2001), Time Series Analysis by State Space Methods, 2nd ed.", Oxford University Press.​

北京天演融智软件有限公司（科学软件网）是EViews软件在中国的授权经销商，为中国的软件用户提供优质服务。