陆 华

(南通市海门区海门港新区实验初级中学,江苏 南通 226100)

摘 要：“新课标”对尺规作图有新的要求,可以概括为要求学生对尺规作图“会画、会认、会用”,这也着重反映于中考试题之中.文章通过对2024年中考真题中尺规作图的命题形式进行分析,得出尺规作图的3类命题形式,并在此基础上总结出教学展望:明确尺规作图的基本概念;经历会画、会认、会用的认知过程;与几何推理相融合.

关键词：新课标;学业要求;尺规作图;中考试题;命题形式

《义务教育数学课程标准(2022年版)》(以下简称《课标》)对尺规作图在结构与学业要求上都发生了变化.在结构上,《课标》采取“化整为零”的方法将尺规作图植入各几何图形的内容之中[1];在要求上,增加了“经历尺规作图的过程,增强动手能力,能想象出通过尺规作图的操作所形成的图形,理解尺规作图的基本原理与方法,发展空间观念与空间想象力”[2].因此,在《课标》颁布之后,尺规作图的研究热度攀升,反映在初中学业水平考试(以下简称“中考”)中,表现为其评价要求与命题形式都发生着变化.在此背景之下,笔者通过对2024年中考试题的分析,总结在新的学业要求之下尺规作图的命题形式,为后续尺规作图的教学提供参考,是提升数学教学质量、落实《课标》的学业要求、培养学生核心素养的重要内容.

1 尺规作图的学业要求

在学业要求中,“经历尺规作图的过程,增强动手能力”,即要求学生会画,学生需要掌握《课标》规定的5种基本作图与14种复合图形作图[3],并能够画出它们的轨迹.“能想象出通过尺规作图的操作所形成的图形”,即要求学生会认,能够根据作图痕迹想象出作图的过程以及所形成的图形,在此基础上进行应用.“理解尺规作图的基本原理与方法”,即要求学生会用,一方面,能够依据所做的图进行几何证明;另一方面,能够在几何证明中利用尺规作图添加辅助线,应用到问题解决的过程中.其中,会画是基础,只有在会画的基础上,才能理解尺规作图的原理和方法,才能会认和会用.会认是关键,它培养学生的几何直观和想象力.正如史宁中教授所说:尺规作图教学,要教想法,要教想象力.会用是将核心素养内化于己的手段.初中阶段增加尺规作图的学业要求,目的是帮助学生通过与具身认知相关的具体的操作活动,经历对几何图形的构造过程,进一步理解组成几何图形的元素之间的相互关系与结构,培养学生的几何直观与空间想象力.

2 尺规作图的命题形式

笔者对现有的60份中考试卷统计发现,有40份中考试卷中涉及尺规作图或单独将尺规作图作为考点,说明各省市中考对尺规作图都比较重视.《课标》要求学生掌握尺规作图的3个层次,中考试题的命题形式总体上也可以分为3种形式.

2.1 会画:单一考查作图技巧

2.1.1 5种基本作图与14种复合图形作图

例1 AC为菱形ABCD的对角线,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹)．

1)如图1,过点B作AC的垂线;

图1 图2

2)如图2,点E为线段AB的中点,过点B作AC的平行线.

(2024年江西省数学中考试题第14题)

例2 如图3,AB与CD相交于点E,EC=ED,AC∥BD.

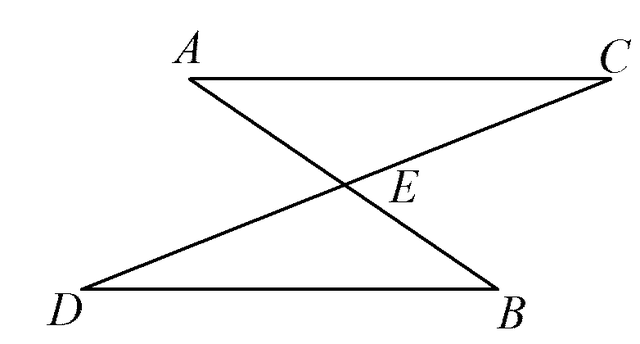
图3

1)求证:△AEC≌△BED;

2)用无刻度的直尺和圆规作图:求作菱形DMCN,使得点M在AC上,点N在BD上(不写作法,保留作图痕迹,标明字母).

(2024年江苏省连云港市数学中考试题第14题)

2.1.2 网格问题中的尺规作图

例3 如图4和图5均是4×4的正方形网格,每个小正方形的顶点称为格点．点A,B,C,D,E,O均在格点上．图4中已画出四边形ABCD,图5中已画出以OE为半径的⊙O．只用无刻度的直尺,在给定的网格中按要求画图．

图4 图5

1)在图4中,画出四边形ABCD的一条对称轴;

2)在图5中,画出经过点E的⊙O的切线．

(2024年吉林省数学中考试题第14题)

评注 只有江西省中考试题单一考查5种基本作图,其他省市的中考如江苏省连云港市数学中考第14题、吉林省数学中考第14题等都是与其他问题相结合进行考查的.因此,单一考查5种基本作图的试题已经逐渐减少,更多的是走向考查复合图形的尺规作图,如山西省中考第21题第3)小题作等边半六边形、陕西省中考第17题作等腰直角三角形、江苏省盐城市中考第25题第2)小题作平行四边形等.尺规作图和网格作图因工具限制不同,作图原理和作图方法也不尽相同,尺规作图是借助直尺和圆规构造线段之间的数量关系,网格作图则是借助正方形网格已有的数量关系来计算和构造出新的数量关系[4],但网格作图其实是尺规作图的一种形式.

2.2 会认:对轨迹或作图过程进行识别

2.2.1 以轨迹识别原理和方法

例4 某班开展“用直尺和圆规作角平分线”的探究活动,各组展示作图痕迹如图6所示,其中射线OP为∠AOB的平分线的有( )个.

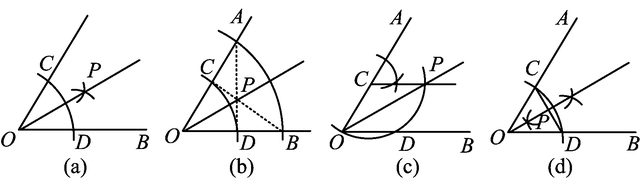
图6

A．1个 B．2个 C．3个 D．4个

(2024年山东省烟台市数学中考试题第7题)

2.2.2 识别轨迹或过程作为已知条件

例5 如图7,在锐角△ABC中,AD是边BC上的高,在BA,BC上分别截取线段BE,BF,使BE=BF;分别以点E,F为圆心,大于

的长为半径画弧,在∠ABC内,两弧交于点P,作射线BP,交AD于点M,过点M作MN⊥AB于点N.若MN=2,AD=4MD,则AM=______.

图7

(2024年湖南省数学中考试题第17题)

评注 这类问题在3种考查形式中是最多的,单纯考查根据作图痕迹去判断是什么的形式很少,更多的是将所要给的条件如角平分线、垂直平分线、中线等改编成尺规作图痕迹的形式,这不仅要求学生判断出是哪一种作图痕迹,还要当作条件进行解题.在40份考查尺规作图的中考试卷中,有14份试卷如此考查,由此看出这一类题目的重要性.

2.3 会用:尺规作图与几何推理相结合

例6 如图8,在Rt△ABC中,CD是斜边AB上的中线,BE∥DC交AC的延长线于点E.

图8

1)请用无刻度的直尺和圆规作∠EMC,使∠EMC=∠A,且射线CM交BE于点F(保留作图痕迹,不写作法);

2)证明第1)小题中得到的四边形CDBF是菱形.

(2024年河南省数学中考试题第19题)

评注 这类问题是在尺规作图的基础上,用尺规作图所得到的条件的进一步证明,解决由尺规作图产生的新问题,可以进一步帮助学生理解图形的性质,考法也较为综合,如江苏省盐城市、扬州市的中考试题都有这样的考法.

3 尺规作图的教学展望

3.1 明确尺规作图的基本概念

在尺规作图时,很多学生受作辅助线的影响,有着用直尺作垂直、作角平分线的不合乎逻辑的做法.因此,明确尺规作图的基本概念是学习尺规作图的第一步.尺规作图,即在几何公理下,有限次利用无刻度的直尺和圆规作出符合条件的图形.因此,尺规作图的工具只能是直尺和圆规,且直尺只能用于过任意两点作直线、联结任意两点和延长任意线段,圆规只能用于画圆或弧、截取一条线段等于已知线段以及截取任意长度的线段.因此,教师在尺规作图教学时,一定要跟学生明确直尺与圆规的功能,在合乎功能的前提下画出的图形才是正确的.当然,也需要让学生知道尺规作图与作辅助线的区别,二者不能混淆.

3.2 经历会画、会认、会用的认知过程

尺规作图的学习也要符合一定的认知过程.类似于概念和命题的学习,也要经历从概念形成、概念辨析到概念应用的过程.因此,一个新的尺规作图的学习也要经历从会画、会认到会用的过程.在课堂教学中,教师要教学生如何依据所学知识进行作图,教授学生画图的想法,在讨论形成作图方法之后,让学生自己跟着步骤动手去画.接着,教师应该举出一些步骤错误的做法让学生辨别其正误或者寻找错因,让学生直观感知该尺规作图的痕迹,加深印象.最后,将该尺规作图置身于一定的问题情境中,试着让学生用尺规作图去解决实际问题,明白该作图的原理与方法,明确其作用.

3.3 与几何推理相融合

尺规作图因其操作简单、能够凸显几何本质、能够明确几何元素与图形之间的关系等优势,逐渐成为了训练和考查学生推理能力的有效着力点.尺规作图也要基于一定的事实,有理有据地进行.几何推理既是尺规作图的原理和方法,也是检验尺规作图正确性的工具.首先,教师在进行尺规作图教学时,一定要基于几何推理去作图,在作完图之后要让学生明白作图的原理和方法,再用几何推理去论证其正确性.其次,在习题设置的时候也可以与几何推理相融合,设置一些与其相关的综合性试题.

《课标》不仅把尺规作图作为一种几何任务,更重要的是将尺规作图作为学生感知几何图形、理解几何图形的性质、培养几何证明能力、探究几何规律的认知工具.因此,它的价值体现在有助于深入理解几何基本要素及其关系,培养学生的空间想象能力、几何推理能力,为数形对应的数学思想与能力提供实操抓手[5].因此,教师要明确它常考的命题形式,融会贯通于教学之中,更好地发挥尺规作图的育人效果.

参 考 文 献

[1] 李卓,代紫涵.落实新课标对尺规作图的新要求:对初中数学教材中尺规作图相关内容修订的若干思考[J].中学数学杂志,2023(12):19-21.

[2] 中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022.

[3] 骆文娟.从《原本》与“课标”谈尺规作图教学[J].数学通报,2022,61(12):17-21.

[4] 江沁,胡典顺.尺规作图与网格作图的比较和启示:以与角相关的两类问题为例[J].数学通讯(上半月),2024(4):4-7;43.

[5] 刘加霞,潘丽云.尺规作图的历史溯源、育人价值及教学建议[J].小学教学(数学版),2022(7/8):20-24.

中图分类号：O123.1

文献标识码：A

文章编号：1003-6407(2024)11-0046-03

* 收文日期：2024-07-11;修订日期:2024-08-16

作者简介：陆 华(1982—),男,江苏南通人,中学一级教师.研究方向:数学教育.