关于拉普拉斯的故事之前数学篇已经讲过了,感兴趣可查阅文末链接。本篇我们只谈数学应用。
希望这篇通过理论➕案例的方式,能让你彻底明白关于拉氏变换的真正意义和价值。
01 什么是拉氏变换
拉普拉斯变换(Laplace transform)是应用数学中常用的一种积分变换,又名拉氏变换,它是任何工程数学课程的重要部分之一。
如果你不知道什么是拉普拉斯变换,也不知道它是如何帮助我们解决许多工程问题的。那只能说,真遗憾,你错了这个世界很美好的事情!也许在你看来,它就是那些似乎只会让你的学校生活变得困难和痛苦的事情。
与其痛苦着,不如干了这杯🍻!
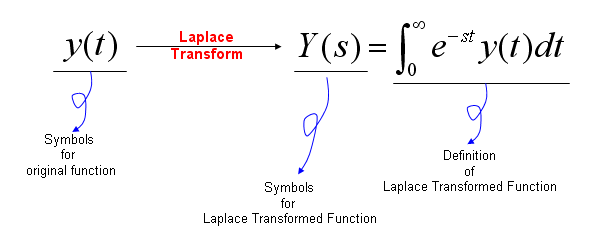
没错,我们封面放的那个图,就是拉普拉斯变换的公式,你可能觉得这个公式真的复杂,为什么一定要设计一个这么复杂的公式出来?

皮埃尔-西蒙·拉普拉斯肖像,Madame Feytaud绘于拉普拉斯逝世后的1842年
皮埃尔-西蒙·拉普拉斯真的是没事干吗?如果这么想!我们就错啦。
其实啊,从哲学角度思考,这个世界就是公平的。如果你想解决一个很复杂的问题,是不太可能用简单的东西去解决(不是绝对)的。
而是一定需要一个平台,足够配得上解决复杂这件事本身的平台先解决90%的问题,然后再用简单的问题处理,才算解决!
什么意思呢?
比如,你要吃饭,完全可以用手刨,但是不文雅!那你就打磨一套精致的瓷器——碗。先把饭装里面,然后再吃,显得也是对饭的尊重嘛。
所以一句话陈述:拉普拉斯变换是把复杂的东西变得简单化了!而我认为就是一座连接两个平行世界的神奇桥梁。
现实中,我们身边有很多现象是随着时间变化的,比如声音的传播、物体的运动等等。而通过时间的变化,我们就能用函数进行表达。
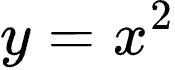
made in latexeditor
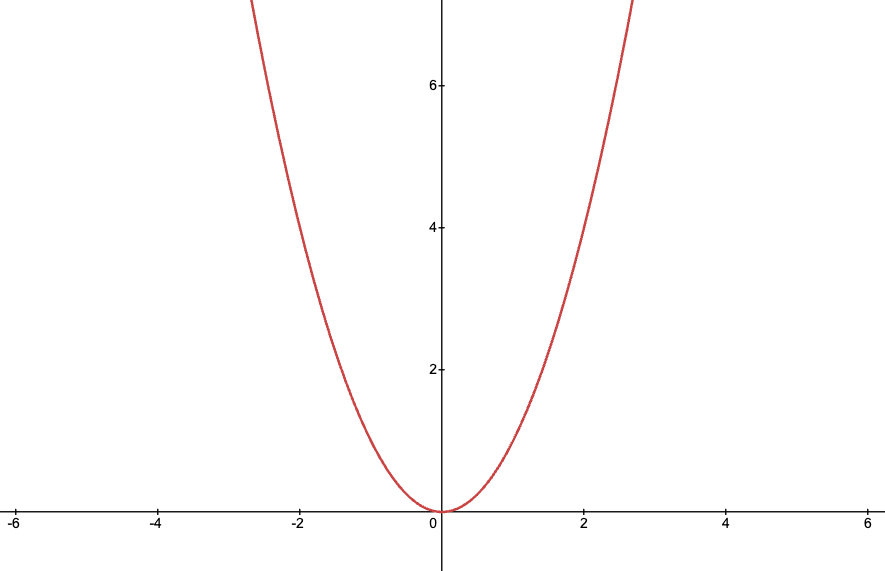
同样的,我们在数学中也有很多不同的函数,比如正弦、余弦和正切三角函数。指数函数,对数函数,双曲函数等。
而x的所有集合,从数学角度,可以称为“域”,而从工程角度来说我们通常把这个域也称为“时间域”。
那么对于这些随时间变化的现象,科学家们发明了一种叫做“拉普拉斯变换”的工具。这种工具就像一个神奇的魔法,可以将复杂的时间变化转换成另一种“域”,也就是频域。这样才使我们更容易理解和分析这些现象。
你可以理解为,事物的本质看不清楚,那就换个角度看清楚了再回到原来的角度。
好,接下来,我们严肃看下这个问题。
02 拉普拉斯变换的数学定义
拉普拉斯变换其实是一个线性变换,线性变换就是一种特别的变化规则,它可以对箭头(向量)做一些变化,比如旋转、拉长或缩短,但必须遵守“加法封闭性”和“数乘封闭性”这两个规则。
拉普拉斯变换是将一个在时间域(即随时间变化的函数)里的数据转换成复频域(频率的世界)里的数据。
在频域里,很多复杂的问题会变得更简单。简单来说,拉普拉斯变换帮助我们把时间域里的复杂现象转化为频域里的简单表达式。
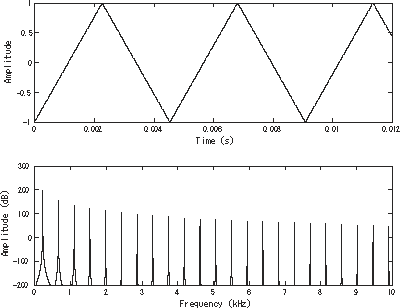
一个三角波在时域(上图)及频域(下图)的图形。三角波的基频为220Hz (后期谈)
什么是时域?
时间域是我们观察随时间变化的事物的方式。例如,小球在地面上弹跳的高度随着时间变化。我们可以画出一个图,横轴是时间,纵轴是高度,这就是时间域的表示方式。
什么是频域?
频域是通过观察事物在不同频率下的表现来理解这些事物。用简单的话来说,频域里的数据告诉我们某个现象在不同“节奏”下的表现如何。
拉普拉斯变换的公式:
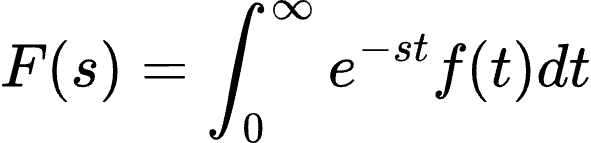
虽然公式看起来有点复杂,但我们可以用简单的方式理解它。
f(t)是时间域里的函数,F(s)是拉普拉斯变换后的结果,s是复数变量。
你可以把这个公式想象成一个“大机器”,它吃进时间域里的数据 f(t),然后吐出频域里的数据 F(s)。
03 简易案例
接下来,我们举个例子:
假设我们有一个小球在弹跳,每次弹跳的高度随着时间逐渐减小。我们在时域里可以用f(t)来表示小球弹跳的高度,假设小球的高度我们用一个简单的指数衰减函数表示:
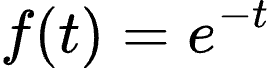
这里的t表示时间,e^{-t}表示随着时间的增加,小球的高度逐渐减小。
好,接下来我们开始拉普拉斯变换!
我们将时间域的函数代入拉普拉斯变换公式中,
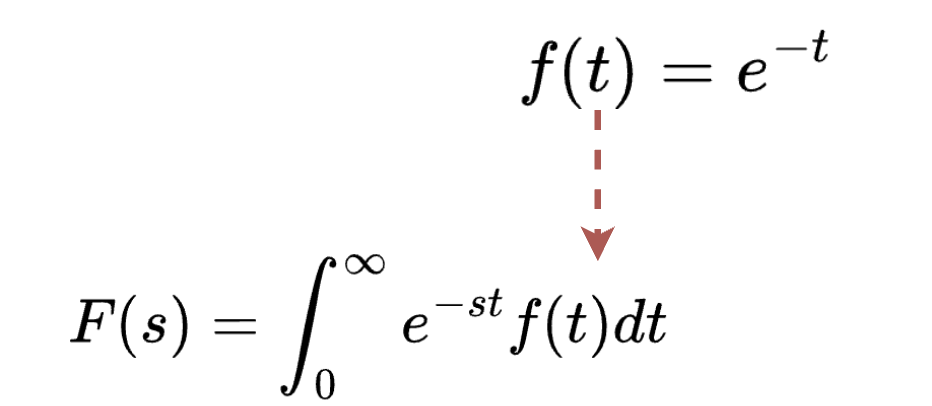
可得:

继续化简:
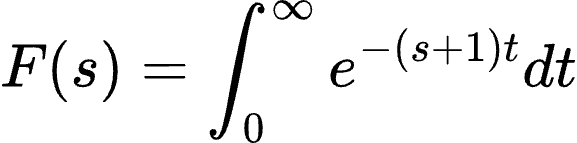
计算这个积分,结果为:
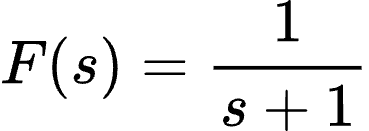
所以,在频域中,F(s)= 1/ s+1,这个结果告诉我们,弹跳的小球的行为在频域里可以用一个简单的函数表示,这使得我们可以更容易地分析和理解小球的运动。
我们看一下对不曲线,如下,
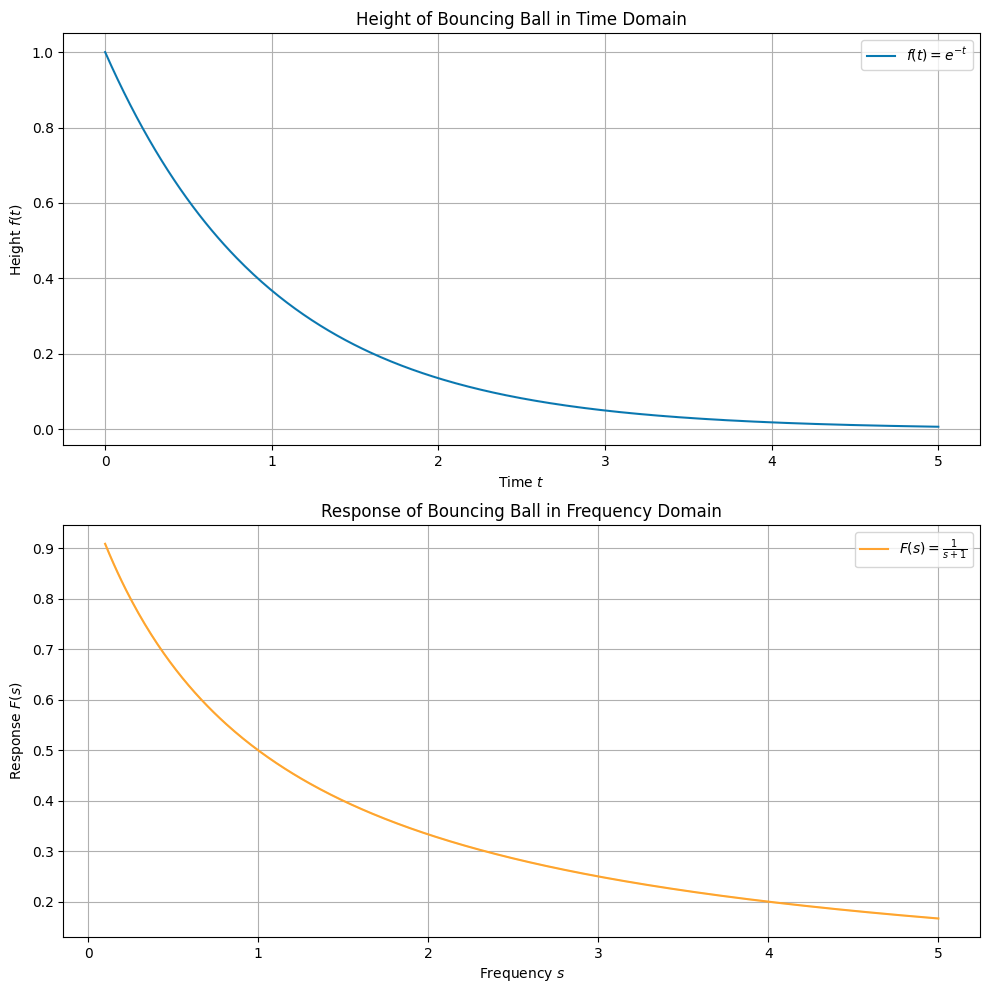
python 制作
第一个曲线是时域曲线展示了小球在每次弹跳后的高度随时间指数衰减。随着时间的推移,小球的高度逐渐减小。
第二个曲线展示了小球在频域中的响应函数。这个函数表示了小球的高度衰减在频域中的表现形式,通过拉普拉斯变换从时间域转化而来。
当然,拉普拉斯变换不仅是一个数学概念,更是工程技术中不可或缺的工具。它的应用帮助工程师们简化复杂问题,提高系统的性能和可靠性。

图片来自AI - MJ
总结:
请相信我,如果你未来是做运动控制算法或电气相关的工程师的话,请提前疼爱拉普拉斯变换。
电路分析、控制系统、信号处理、通讯系统必绕不开的。
在未来的学习和工作中,灵活运用拉普拉斯变换将为你提供强有力的支持,使你能够更好地解决各种工程和科学问题。
希望通过本文的总结,你能更好地理解拉普拉斯变换的价值和广泛应用。


今天教大家一个炼金术式F(X)=∮e^s*(1+n)^n*dt,此式能炼出金棍银棍和鉮棍,大家学废了吗