在真正随机的彩票中赢钱是很难的。一开始，它的随机性可能是一个绊脚石，但当你深入研究它时，它可能会成为你作为彩票玩家的垫脚石。你不妨感谢彩票是真正随机的。

我脑子里突然冒出一个想法，如果用一幅图来描述彩票的随机性，它会是什么样子呢？

很快，我就编写了一个计算机模拟程序。实现目标的方法之一是模拟随机彩票抽奖过程并绘制出一幅图像。

这就是我得到的照片：

乍一看可能不太明显，但该图暗示了在玩彩票时不要犯数学错误的具体想法。它表明彩票游戏在一定程度上具有数学确定性。

我们稍后会深入探讨这一数学策略。不过，现在让我给你一个提示：

真正的数学乐透策略就是做出明智的决定。通过计算所有可能的选择并做出明智的选择，实现最佳的成功率和失败率。

请注意，有了这种数学策略，你应该庆幸自己玩的是真正随机的彩票游戏。如果彩票不是完全随机的，那么任何概率计算都不可能正确。

科学只知道两种类型的过程：确定性和随机性。如果将两者结合起来，就会得到概率性的东西。

我们大多数人不明白彩票是如何运作的，因为大多数彩票玩家仍然认为统计数据是分析彩票的正确工具。例如，人们会寻找热门数字和冷门数字。

纠正这个错误观念的时机已经到来，因为当涉及有限数字时，您不会使用统计工具。由于彩票的可能性是有限的，因此我们对其可能结果提出的任何问题始终是组合问题，并且需要解决一个概率问题。

这是否意味着我们可以预测彩票？

如果你指的是下一个中奖号码，那当然是不可能的。但如果我们试图从大数定律的角度预测真正随机的彩票游戏的一般行为，那么是的。这在数学上是可能的。

在像彩票这样具有有限可能性的随机事件中，实际结果总是与概率计算一致。

因此，彩票是确定性的，因为随机抽奖遵循概率规则。这个结论在许多方面都很有用（例如，如何在大多数抽奖中减少错误）。

这就是数学信息的重要性。当你知道所有可能性时，你就有能力做出明智的选择，你永远不会犯数学错误。成功与失败比率的计算就是一个例子。

因此，完全随机性是做出数学预测的必要条件。

但请不要误会我的意思。即使是1-2-3-4-5-6也和其他组合一样有可能。本文本身并不是关于概率的。

这就是我们经常接触概率而完全忘记赔率概念时的问题。赔率和概率在数学上并不等同。我们将在下面详细讨论两者之间的巨大差异。

让我们回到彩票随机性的图片（如上所示）。首先，注意条纹和聚类的证据。为什么会出现这种聚类现象？

好吧，聚类是随机数据的固有特性。但这不是重要的问题。最重要的是信息。

你应该问“它告诉我什么？ ”

这幅画背后的故事远比我们看到的要多。

敬请关注，因为本文将解释为什么真正随机的彩票在数学上是可预测的。

这将是一篇很长的文章。所以请做好准备。

让我们开始。

我想到了一个问题：我该如何描述彩票的随机性？

我读过史蒂芬·平克的著作《人性中的善良天使》，也看过博·艾伦的这幅视觉对比图。

但我想要一些能够反映随机彩票本质的东西，并选择一种我可以解释的策略。

这不是一件容易的事。但我有一个明确的目标：前进的唯一途径就是从某个地方开始。

首先，我选择了一种最小的彩票游戏格式。20选5彩票游戏只能产生4845种可玩组合，所以我认为这种格式相当容易管理。

幸运的是，虽然彩票规则可能因运营商而异，但抽奖机制是相同的。

每次挑选一个球，同时球会在转筒内进行洗牌。每挑选一次，转筒中的球就会减少一个。以此方式继续抽奖，直到完成获胜组合。

因此，如果我必须创建一个模拟程序，它必须执行以下操作：

程序将绘图结果保存在数据库中。这个过程必须运行一千多次才能获得足够大的数据集进行分析。

这个大型数据集将有助于从大数定律的角度提供确凿的证据。从这个大型数据集中，程序将计算多次抽取的每个组合的观察频率，并以特定方式直观地提取信息。

第一个方格代表1-2-3-4的组合。17-18-19-20将占据最后一个方格。

在模拟测试中，每次抽取一个组合时，灰色代表出现一次，然后随着出现次数的增加，颜色会变深，直到变成红色。红色表示该组合被抽取了十次以上，白色表示从未被抽取过，频率为零。

这看似一个简单的想法，但说起来容易做起来难。首先，我需要确保几件事做对了。一个问题是模拟器将使用的随机过程的质量。

当我们让计算机生成随机数时，我们使用伪随机数生成器，简称PRNG一台精确的机器怎么可能偶然生成数字呢？计算机很难生成随机数，因为它盲目地遵循指令，它产生的任何输出都必须是可预测的。

然而，随机过程无处不在；因此，计算机科学家必须接受它们。

因此，我使用了几种实用的实现方式来创建一次又一次的随机性。然而，当可预测性至关重要时，其中一些方法并不适用。

看一下以下PHP5代码片段：

mt_srand(1053114994);

for ($i=1; $i<=10; $i++) {print mt_rand().'<br>’;}

上述脚本将产生以下数字：

你能看出其中的规律吗？

人们可以很容易地知道列表中的下一个数字。只需确定用于生成数字的初始种子即可。

PRNG可以生成看似随机的数字，但实际上，它们是可预测的。如果我在不同的机器上运行相同的脚本，我总会得到相同的结果。

让我直观地向您展示PRNG在模拟程序中的确定性。

我必须向您展示它是什么样子的，因为您必须看到非随机图片和真正随机图片之间的区别。

使用20选5乐透格式，计算机模拟器的可预测性如下：

伪随机数生成器模拟程序在两台不同的机器上运行时显示相同的条纹和聚类模式。

你能看出聚类模式没有改变吗？每次计算机运行时，模拟器都会绘制相同的组合。

在1000次抽奖中，模拟程序将频率分布在896种组合中。但是，如果运行3000次抽奖，该程序似乎会从相同的组合中挑选数字。

因此，聚类模式是恒定的。尝试比较角点。

如果彩票游戏是这样运作的，你马上就会发现其中有漏洞。你所要做的就是从这896个组合中挑选你的组合，其他的就不用管了。因此，中奖只是时间问题。

彩票运营商使用真正的随机数生成器程序。但我们怎么知道呢？最好还是问一问。对于彩票玩家来说，你们有权知道。

大多数玩家不知道从计算机代码层面数字是如何随机生成的。

回到随机生成器，彩票模拟程序需要一个真正的随机过程。如果我想准确了解真正随机的彩票，粗心大意是我最不应该做的事情。

在创建彩票模拟程序时，必须考虑一个公正且不可预测的过程。这一目标对于彩票和所有类型的赌博尤其如此。

一种方法是将外部随机数据引入计算机系统，为PRNG提供种子并重新播种。

我想到的一个简单方法是计算我的某个网站的点击量。人们访问和点击某个网站的时间点是完全随机且不确定的，因此，它们可以成为具有一定熵值的随机信息的良好来源。

计算机技术已经如此进步，您已经有多种不错的选择。

一种方法是利用物理现象。例如，你可以使用连接到计算机的盖革计数器测量放射性衰变。

我正在考虑可以立即用于我的随机测试生成器的东西。

幸运的是，如今的编程语言已经发展到可以解决随机性问题。

PHP7引入了加密安全的伪随机数生成器或CSPRNG ，其特性使得数字生成不可预测。

可以使用random_int指令轻松调用。

很高兴知道我们有一个更便宜并且随时可用的解决方案。

然而，必须进行一系列统计测试以确保随机生成的高质量。

由于使用PHP7可以实现实用选项，因此我的下一步是检查CSPRNG是否兑现了其承诺。

第一个测试是检查代码产生的随机分布是否遵循大数定律。

在彩票中，所有数字的概率都相等。根据大数定律，如果实验重复多次，所有数字都会收敛到相同的预期值附近。因此，模拟程序必须能够产生相同的特性。

如果我们有一组20个数字，每次挑选一个，那么每个数字的概率为1/20，或者100次抽奖中的预期值为5。如果我们挑选一百万次，那么每个数字的观察频率应该在50,000左右。

使用random_int迭代一百万次，从1到20抽取数字。所有数字都收敛在50,000左右。

上表看起来不错。但我们可以使用下面的饼图更直观地查看它：

如您所见，每个数字都获得了相同的份额，这表明选择是公正的。Random_int通过了第一项测试。

接下来，我们将检查随机生成的数字的质量。需要检查结果与预期值的接近程度。

检查的最佳方法是将random_int与流行的掷骰子实验中名为mt_rand 的非CSPRNG对应项进行比较。

一个骰子有六个数字。每个数字的概率为1/6。如果我们同时掷三个骰子一百万次，计算机程序必须能够非常接近地重现以下预期值：

我必须使用一系列统计结果来比较两个PHP7函数。

以下是第一次运行的初步结果：

可以看出，这两个函数与预期值非常接近。表格显示random_int表现更好。但是，为了进行比较，需要多次重复测试。

以下是我的样本测试的完整列表：

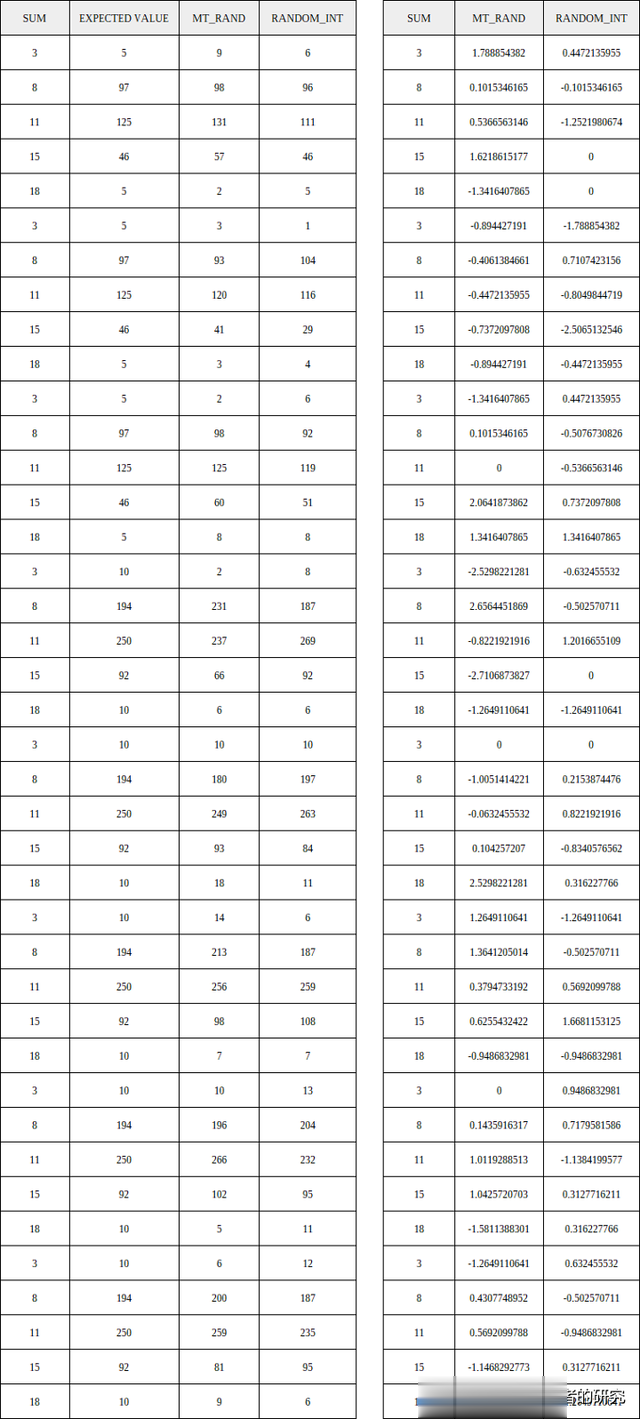
我们可以通过下图直观地看到两个随机函数之间的相互关系：

为了确定哪个产生更好的随机数，我们必须寻找更接近零线的那个。从图中可以看出，CSPRNG的random_int在质量测试中胜出。

我的初步测试表明，我可以使用random_int指令继续模拟真正随机的彩票游戏。

我采用了20选5抽奖形式，但是只预测4个数字，太多预测更加困难。

您将期望彩票模拟程序不会产生偏差且具有可预测的聚类模式。

这意味着甚至需要出现那些不寻常的组合，例如1-2-3-4、17-18-19-20或5-10-15-20。

如果我们给彩票足够的机会，真正的随机抽奖必须允许所有组合发生。根据真正大数定律，即使是最不寻常的组合、巧合和罕见事件也必须发生。

换句话说，连续看到一系列不太可能的组合并不令人惊讶。

现在让我向您展示我的模拟程序的结果：

独立进行了四次模拟测试。每次运行都表现出不可预测的条纹和聚类模式。所有模拟测试都使用CSPRNG。

我们继续观察最多5000次抽奖的行为：

在5000次抽奖中，您无法指望所有4,845种组合都会被抽出。大约需要40,000到50,000次抽奖才能抽出所有4,845种组合。

让我们继续抽奖15000次。

在15,000次抽签中，某些组合出现的频率高于其他组合。而且许多组合仍未抽签，正如空格的存在所表明的那样。

你可能会问，为什么还有227种组合尚未发生？概率论有一个答案。我们稍后会讨论这个概率原理。

注意，在这个阶段，你开始看到红色的方块。这些组合已经画了十多次了。

快进到45,000次绘制；模拟图像如下所示：

你会注意到，在这个阶段，所有组合都已经抽出来了。正如我之前所说，随机抽奖必须遵循真正大数定律。

如果我们给彩票足够的机会，真正的随机彩票抽奖必须允许所有组合发生。根据真正大数定律，即使是最不寻常的组合、巧合和罕见事件也必须发生。这意味着即使是1-2-3-4或2-4-6-8也应该发生。

组合有不同的成分。我们将具有相同成分的组合放入组合组中。

这些组合组具有不同的成功失败率。这些具有最佳成功失败率的组合是彩票抽奖中的主导组合。

当你了解所有可能性时，做出正确的选择很容易。

彩票由三种组合组成——主导组合、偶然组合和罕见组合。

您不想把钱花在一个经过5000次尝试后只给您一次有利机会的团队上，对吗？

作为彩票玩家，您的目标不是操纵随机游戏。相反，您的目标是通过玩主导组合来发挥出最佳水平。成功失败率会告诉您是哪一种。

如果您想了解彩票游戏中的主要组合模板，那么统计数据并不是合适的数学工具。

统计数据经常会失败，因为它们会诱使你相信某件事是有效的，直到有足够的数据证明它是错误的。

概率和统计是两个截然不同的概念，它们以不同的方式处理问题。主要区别在于我们所知道的内容。

因此，根据我们的知识，问题可能是统计问题，也可能是概率问题。

例如，我们有一盒20颗弹珠。我们知道盒子里有黄色、青色、灰色和绿色的弹珠，但我们不知道每种颜色有多少颗。

由于我们不知道这20颗弹珠的成分，因此我们使用统计工具根据随机样本推断它们的成分。

如果我们知道有五颗黄色、五颗青色、五颗灰色和五颗绿色弹珠，那么我们遇到的任何问题都是需要解决的应用概率问题。

因此，利用概率，我们可以提出如下问题：

我们抽出一颗黄色弹珠、两颗青色弹珠和一颗灰色弹珠的可能性有多大？或者我们抽出全部四颗绿色弹珠的概率是多少？换句话说，当我们的知识足以回答问题时，我们就不需要统计分析。

同样的理念也适用于彩票。

我们可以问：我们抽到1-2-3-4的概率是多少？

这个问题只需将问题重新表述为：抽出2个低奇数和2个低偶数的概率是多少？

因此，我们只需计算概率就能得到答案，不需要随机样本或统计分析。

这就是彩票中的概率原理。它也适用于各种彩票系统，无论是5/50、6/49、6/42还是5/35。

概率为你提供了强大的知识来指导和帮助你获得最佳的拍摄效果。

令人惊讶的是，尽管早在1700年法国著名数学家布莱斯·帕斯卡和皮埃尔·德·费马就发现了概率论，但一些团体仍然使用统计数据来分析彩票游戏。

然而，有趣的是，一个多世纪以前，意大利博学者、数学家和赌徒吉罗拉莫·卡尔达诺早在帕斯卡和费马之前就找到了概率问题的数学解决方案。

现在该是你改变看待彩票的方式的时候了。

当然，如果没有数学的另一个分支——组合学的帮助，彩票中的概率分析是不完整的。

当然，我说的不是预测下一个中奖号码，而是从大数定律的角度来谈彩票的全貌，后面你会发现，你可以看到你的游戏未来的走势。

只要有足够多的机会，概率计算总是数学上的确定性。

现在让我们讨论一下组合数学和概率论如何作为乐透策略协同工作。

在本文中，我并不是在谈论确定确切的获胜组合。相反，我在讨论预测主导中奖抽奖的确切组合模板。根据大数定律，随着抽奖次数越来越多，相同的模板将继续占主导地位。

根据大数定律，我们可以预计模板＃1将主导彩票抽奖，并且随着抽奖的增加继续主导20选5游戏。

模板＃1的概率值为0.1289989680。

要预测此模板的预期频率，请将概率乘以抽取次数。

预期频率（模板#1）=0.1289989680x预期抽取次数

例如，在100次抽奖中，我们预计模板#1会出现大约13次。

预期频率（模板#1）=0.1289989680x100=13

在1000次抽奖中，我们预计该模板会出现129次。

预期频率（模板#1）=0.1289989680x1000=129

那么，在5000次抽奖中，模板#1将出现645次。

预期频率（模板#1）=0.1289989680x5000=645

对其他模板进行相同的计算，您会发现模板＃1随着时间的推移占据主导地位。

为了说明，让我们比较模板#1与模板#2，并直观地显示差异。

在下面的视觉比较中，模板#1用红色表示，模板#2用蓝色表示。请注意，模板#1在所有图像中都占主导地位。

100次抽奖

模板#1预计会出现13次，而模板#2预计会出现5次。

预期频率（模板#1）=0.1289989680x100次抽签=13

预期频率（模板#2）=0.0515995872x100次抽取=5

实际抽签结果显示，概率估计非常接近。我们不能指望预测结果会一致，因为概率论只是一种数学指导。但它是否是预测两个模板可能结果的可靠工具？答案是肯定的。

500次抽奖

在500次抽奖中，模板#1应该出现大约64次，而模板#2应该出现大约26次。

预期频率（模板#1）=0.1289989680x500次抽取=64.49

预期频率（模板#2）=0.0515995872x500次抽取=25.79

看，实际抽奖结果非常接近。让我们继续进行1000次抽奖。

1,000次抽奖

预期频率（模板#1）=0.1289989680x1000次抽取=128.99

预期频率（模板#2）=0.0515995872x1000次抽取=51.59

和往常一样，实际开奖结果总是与概率计算结果一致。根据大数定律，模板#1必须主导20选5乐透游戏的结果。从数学上来说，彩票服从概率论的支配是确定的。

随着图画越来越大，从3000幅到5000幅，进行视觉比较。

3,000次抽奖

预期频率（模板#1）=0.1289989680x3000次抽签=386.996904

预期频率（模板#2）=0.0515995872x3000次抽取=154.7987616

5,000次抽奖

预期频率（模板#1）=0.1289989680x5000次抽取=644.99484

预期频率（模板#2）=0.0515995872x5000次抽取=257.997936

对于20选5的游戏，建议玩家选择主导模板#1。

下面的视觉比较将证明这一点：

模板#1VS模板#5，5000次抽奖（模板#1获胜）

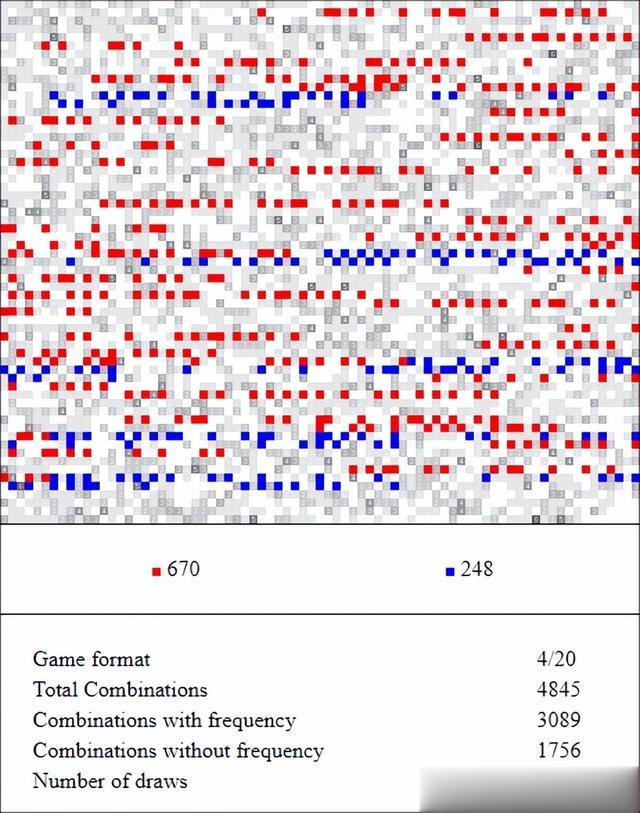
模板#1VS模板#10（5000次抽奖中，模板#1获胜）

模板#1VS模板#15（5000次抽奖中，模板#1获胜）

模板#1VS模板#20（5000次抽奖中，模板#1获胜）

模板#1与模板#25在5000次抽奖中的表现（模板#1获胜）

模板#1VS模板#30（5000次抽奖中，模板#1获胜）

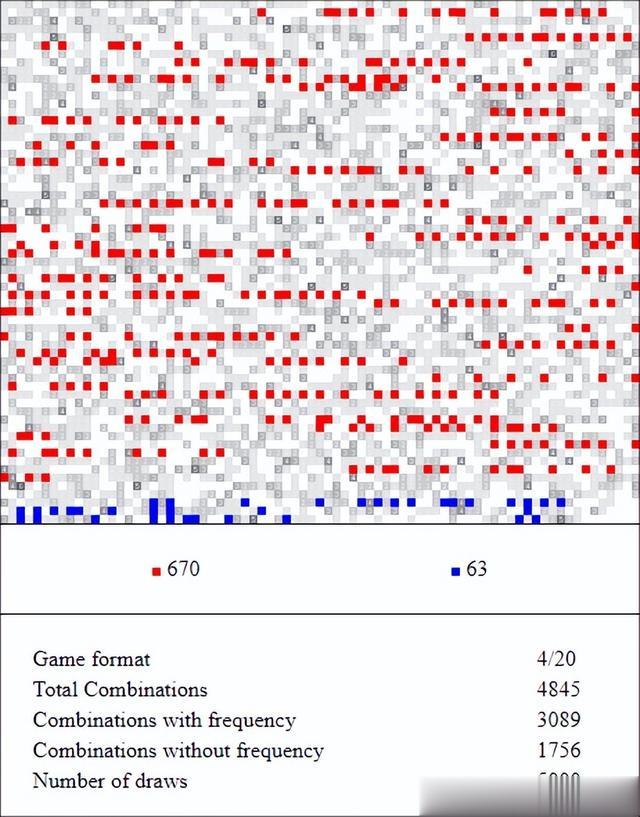
模板#1VS模板#35（5000次抽奖中，模板#1获胜）

上面的图表表明您不必担心其他所有模板。如果您坚持使用模板1，您将获得最佳拍摄效果。

尽管彩票可能确实是随机的，但在一定程度上它可以在数学上具有确定性。

您需要一个系统来提供选择数字的详细指南。组合学和概率论将非常有用。但是，在数字较大的随机彩票中，计算可能过于详尽和繁琐。这就是为什么提供彩票计算器来完成繁重的工作。

彩票结果中的随机性和确定性是如何结合的？

在彩票游戏中，每次抽奖中抽出的具体数字都是随机且不可预测的。相反，固定规则和可能组合的数量决定了游戏的整体结构和赔率。这种有限结构让位于彩票游戏的确定性，这反过来又允许应用数学原理来了解彩票球随时间的变化。

彩票中的确定性过程与随机过程有何区别？

在彩票中，确定性过程是指组合组根据其组成而变化的成功与失败比率。这些组合组表现出可预测的结果。相反，随机过程以实际抽取的数字为例，它是不可预测的并且每次都有所不同。将这两个过程结合起来有助于彩票结果的整体概率性。

大数定律和彩票有何关系？

在彩票游戏中，尽管组合的概率相同，但由于其组成和成功失败率各不相同，因此组合的概率并不相同。根据的计算，某些组合更有可能占据主导地位，并且随着抽奖活动的增多，这种局面将继续存在。作为一名彩票玩家，您的目标应该是跟随占主导地位的组，以最大限度地提高您的获胜机会。

如何从数学上解释彩票结果的可预测性？

彩票结果的可预测性在数学上基于不同组合组的不同成功失败率。虽然每次抽奖的具体结果是随机且不可预测的，但不同组合组随时间推移的总体表现反映了游戏的确定性，这可以通过其成功失败率来计算。

某些组合组是否更有可能主导彩票抽奖？

是的。由于组合的组成不同，因此它们表现出不同的成功失败率。这意味着一些组合组更有可能主导彩票抽奖，并且随着抽奖活动的增加将继续表现出主导地位。作为彩票玩家，您的目标应该是跟随这个主导组以获得最佳机会。