在原子系统中，电磁诱导透明度由量子干涉效应或法诺相互作用诱导，由于具有外部控制激光场的相干驱动原子波包。OMIT是一种类似于EIT的现象，首先在理论上被预测，然后通过实验验证，在腔光机械系统中，这是由内部场的不同途径之间的破坏性量子干涉引起的。最近，OMIT的研究引起了广泛的关注。

例如，单光子路由器、超慢光传播、量子基态冷却、精密测量、布里渊散射诱导透明度和非互易光存储、光机械诱导放大、有效的质量传感，控制光子在无损介质中的传播17，光机械诱导随机共振18和混沌传递和奇偶校验时间对称微谐振器。

此外，可调EIT和吸收20、极化子状态以及从封锁到透明度的过渡还研究了电路中的QED系统。另一方面，关于OMIT的研究已经扩展到双光和多光诱导透明度23通过集成更多的光学或机械模式。

据报道，原子介质辅助光机械系统中可能会出现多个OMIT窗口、多谐振器光机械系统带N膜的光机械系统，两个耦合的光机械系统和多腔光机械系统。特别是多路OMIT现象的实现在多通道光通信和量子信息处理中显示出许多实际应用，这激发了对这种OMIT的进一步研究。

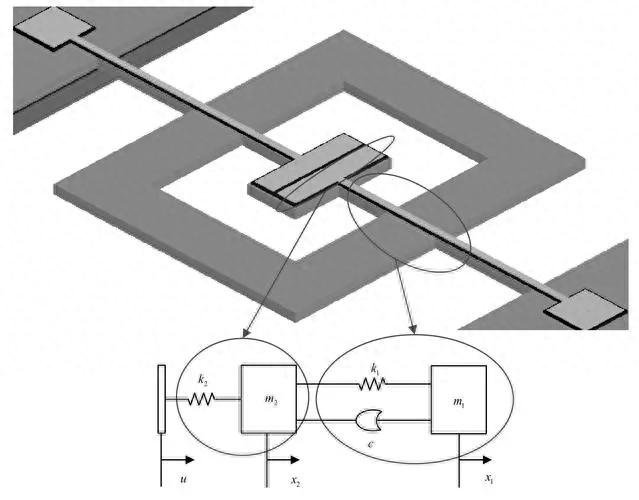
理论模型和哈密顿算符：正在考虑的1D MCOS如图所示。1.腔体光机械阵列的第N个腔体由频率ω的强控制场相干驱动c和频率ω的弱探头激光场p. N 个光机械腔标记为 1、2、...、N。第j腔和第j个机械振荡器的频率用ω表示j和 ω美杰分别。

第j腔与第j机械振荡器的耦合强度为g美杰和 gn是第n 个和第 （n + 1） 个腔 \（（n\ne N）\） 之间的跳跃速率。此外，一对DDI阶梯型三能级里德伯原子在第i个腔中得到辅助。我们系统的里德伯原子可以选择铯原子，精细结构状态|6S1/2， F = 4〉 和 |6P3/2，F′ = 5〉 可视为基态 |g〉 和中间状态 |e〉，而对应的里德伯状态 |r〉 假定为70S1/241。

至于第一个里德伯原子，频率控制场ωc耦合到 \（|e\rangle \leftrightarrow |r\rangle \） 转换，具有 Rabi 频率Ω和频率失谐 Δr.第 i 个腔场驱动强度为 g 和频率失谐 Δ 的 \（|g\rangle \leftrightarrow |e\rangle \） 跃迁e.简而言之，由于里德伯态的长寿命（τ≥1μs），假设第二个里德伯原子在第i个腔（100 ≤ i ≤ N）中被DDI激发，并与第一个里德伯原子耦合。

当阻塞半径小于一对里德伯原子的原子间距离时，这种构型具有实验可行性，然后它们可以同时被激发到里德伯态，并通过范德华类型的DDI利用它们的相互作用。

光学模式被描述为湮灭（创建）算子cj(\（{c}_{j}^{\dagger }\））第 j 个腔场，以及 \（{b}_{j}^{\dagger }\）（bj） 是第 j 个机械谐振器的创建（湮灭）算子。Δj= ωj− Ωc是第j个腔场与控制场的失谐，Δ = ωp− Ωc表示探测场和控制场之间的失谐。

Δe= ω例如− Ωj, Δr= ω再− Ωp和 ωμν表示能级之间原子跃迁的频率 |μ〉和级别 |ν〉（μ， ν = g， e， r）.\（{\sigma }_{\mu \nu }^{（k）}\equiv |\mu {\rangle }_{kk}\langle \nu |\） 是第 k 个 （k = 1， 2） 里德伯原子的投影 （μ = ν） 或跃迁 （μ ≠ ν） 算子。 此外，输入场的哈密顿量包括控制场和探针场的哈密顿量。εc是控制场的幅值和εp是探头场的振幅。

第一项对应于两个相邻空腔之间的跳跃和gn是腔间隧穿强度。第二项描述第j个腔体与机械振荡器之间通过辐射压力和g的相互作用美杰是耦合强度。其中一个与控制场和第i空腔场相互作用的里德伯原子分别列在第三项中。V（R）是两个里德伯原子之间的DDI强度，被描述为最后一项，R是两个里德伯原子之间的距离，可以通过单独的光学陷阱控制在不同范围内。

其中 κj和γ美杰在现象学上引入，分别表示第j个腔的耗散和第j个机械振荡器的衰减速率。S = V（R） 与 \（{\bar{\sigma }}_{rr}^{（2）}=1\） 由于假设第二个里德伯原子在与第一个里德伯原子的相互作用过程中被激发到里德伯态的原因。γμν 是电平 |μ〉和级别 |ν〉。

此外，\（{\tilde{{\rm{\Delta }}}}_{j}={{\rm{\Delta }}}_{j}-{g}_{mj}{\bar{\lambda }}_{j}\）。\（{\bar{\lambda }}_{j}\） 的一般形式将在下面给出。为了获得稳态解，这些解对参数中的控制场进行了严格的要求εc并在参数ε中更正为一阶p的探测场。由于探测场比控制场弱得多，因此可以使用 ansatz 近似写算子 O 的平均值46。

输出字段：系统的响应可以通过探头频率处的输出场来检测，可以通过腔体的标准输入输出理论表示如下。

{\varepsilon }_{out，p}{e}^{-i{\rm{\Delta }}t}+{\varepsilon }_{p}{e}^{-i{\rm{\Delta }}t}+{\varepsilon }_{c}=2{\kappa }_{N}\langle {c}_{N}\rangle 。

{\varepsilon }_{T}=\frac{{\varepsilon }_{out，p}}{{\varepsilon }_{p}}+1=\frac{2{\kappa }_{N}{c}_{N，-}}{{\varepsilon }_{p}}={\chi }_{p}+i{\tilde{\chi }}_{p}。

在这里，χp= Re（εT） 和 \（{\tilde{\chi }}_{p}={Im}（{\varepsilon }_{T}）\） 分别表示与吸收和色散相关的输出场的同相和异相正交。省略是吸收和分散同时消失的现象。输出场的这两个正交可以通过零差技术测量。使用方程，可以很容易地得到\（{c}_{N，-}\），然后输出字段的表达式εT以建设性的形式给出。

其中 \（{B}_{j}={\kappa }_{j}-i{x}_{j}+\frac{|{G}_{mj}{|}^{2}}{{\gamma }_{mj}-i{x}_{j}}（j=1，\ldots ，N）\）.在上式中，分母的第一行描述了衰减率κN和 κN−1通过耦合强度 G 耦合N−1.分母的第二行描述了两个空腔与衰减率κ的相互作用N−1和 κN−2并且联轴器强度为gN−2等等。

很明显，分母的每一行都包含一个由有效耦合 G 表示的交互作用项美杰在机械振荡器和腔体之间。从分析上讲，我们注意到当 G美杰= 0，机械振荡器不与第j个腔体耦合。

此外，B 中的额外项 A我线表示空腔场与包括DDI在内的一对里德伯原子的相互作用，其一般形式如下表所示，Q = （γ克+ iδr+ iS） （γ通用 电气+ iδe) + Ω2， \（P=i（{{\rm{\Delta }}}_{r}+S-{{\rm{\Delta }}}_{e}）+{\gamma }_{er}+\tfrac{G{e}^{2}（{\gamma }_{ge}+i{{\rm{\Delta }}}_{e}）}{（{\gamma }_{gr}+i{{\rm{\Delta }}}_{r}+iS）\。

（{\gamma }_{ge}+i{{\rm{\Delta }}}_{e}）+{{\rm{\Omega }}}^{2}}\）和\（{G}_{e}=g{\bar{c}}_{i}\）是里德伯原子和空腔场之间的有效耦合强度。 当然，当一个人将原子捕获在第一个空腔中时，这个术语将出现在最后一行。如果里德伯原子定位在第N个空腔中，它将出现在分母的第一行。

没有里德伯原子：在本节中，我们首先关注由于腔场和没有里德伯原子的机械振荡器之间的相互作用而产生的多重OMIT现象。参数为 ω锰/g美杰= 20， γ锰/g美杰= 0.001， κN−1/g美杰= 0.002， κN/g美杰= 2，我们假设 \（{G}_{mN}/{g}_{mj}={\bar{c}}_{j}=1\）。

光机械耦合参数g美杰= 1 kHz 基于真实的腔体光机械系统7.为简单起见，以下输出场的吸收分析仅限于具有四个腔的混合系统。可以按照上述基于方程的相同方法推广到大量腔体情况。

首先，图片说明了吸收Re（εT） 的输出字段作为 x/κ 的函数N对于四个腔。详细地，图。图2（a）仅描述了一个耦合到第一个腔体的机械振荡器。

（c）对应于分别耦合到腔1、2和3的三个机械振荡器。（d）描述了耦合到四个空腔的四个机械振荡器。吸收线的凹陷对应于输出字段的透明窗口。

可以发现，透明窗口的数量依次随着机械振荡器的增大而加一个，这是由方程的无穷大分母确定的耦合参数g的外观N−1和 G锰在分母中。当混合系统有N个空腔和N个机械振荡器一个接一个地耦合而不考虑外部环境的影响时，透明度窗口的总和加到2N − 1。

因此，MCOS在2N − 1个不同频率下对探测场变得透明，这是输入探测场与多个空腔内耦合腔场相互作用以及耦合腔场与机械振荡器之间的相互作用产生的反斯托克斯场之间的破坏性干扰。然而，当N变大并且每个腔都与其浴耦合时，数值结果表明该系统的多个透明窗口变得越来越不透明。因此，我们关注的只是实际实验中的小系统。

多个OMIT窗口的起源可以用不同能级路径之间的量子干涉效应来解释，图中给出了由N个空腔和N个机械振荡器组成的混合系统的能级配置。3. 探针场的激发途径是量子干涉不同的耦合途径G美杰。因此，对于N个腔和N个机械振荡器，量子干涉路径的总和为2N − 1。此外，这些破坏性量子干涉的路径是通过光机械相互作用和隧穿形成的，在εT在极值点≈ 0。

为了进一步探索机械振荡器相互作用产生的OMIT特性，我们绘制了吸收Re 的输出字段作为 x/κ 的函数N适用于一个和两个耦合振荡器的情况。图中还显示了没有机械振荡器耦合的情况，以便进行比较。

由于机械振荡器的路径与腔场之间的相消干扰，如果第一个腔体与机械振荡器耦合，系统将增加一个新的透明窗口，用图片（a）（b）可以发现，第三标记的机械振荡器刚好拓宽了中心吸收峰。另一方面，（c）描述了机械振荡器和第二腔之间的耦合。

图片（d）描述了机械振荡器分别与第4和第2腔相互作用。可以发现，偶数标记的机械振荡器不会改变两种情况下透明度窗口的数量，与没有机械振荡器耦合的情况相比，只有助于扩大中心吸收骤降。请注意，尽管所有机械振荡器都是相同的，但它们仍然可能导致不同的量子干涉路径。

数值计算表明，如果放大空腔和奇数标记的机械振荡器的数量，则结果与上述结果相似。详细地说，对于奇数标记的情况，无论有多少机械振荡器与空腔耦合，与没有机械振荡器耦合的情况相比，透明窗口的数量仅增加一个。

增加的奇数标记机械振荡器仅略微改变中心吸收峰的宽度。而对于偶数标记的振荡器，增加的振荡器仅改变中心吸收峰值或骤降的宽度。这些行为可以从方程进行分析。ε的等式T≈ 0 有 N − 1 个不同的根，在极值点没有耦合的机械振荡器。

对于奇数标记振荡器及其腔体，εT≈ 0 最多有 N 个不同的根。此外，当只有奇数或偶数标记振荡器与空腔耦合时，我们还发现增加有效光机械速率G锰，中央吸收峰或下降将显着扩大。

总之，我们研究了MCOS的省略。对于没有里德伯原子被困在腔中的情况，MCOS系统已经证明，当N个空腔分别与N个机械振荡器相互作用时，输出场会产生2 N − 1个省略窗口。但是奇数标记和偶数标记振荡器会导致不同的效应，如果出现奇数标记振荡器，则量子干涉在吸收曲线中只出现一个额外的OMIT。

相比之下，增加的偶数标记机械振荡器只是扩大了中心吸收骤降或峰值。在这种情况下，相应的透明度窗口可以通过提高有效光机械速率从OMIT更改为ATS。

另一方面，当两个里德伯原子被困在第i个DDI较弱的空腔中并且空腔与机械振荡器耦合时，可以观察到两个额外的OMIT窗口。此外，随着DDI强度的增加，两个额外的OMIT窗口将逐渐转向远非共振状态。正确的额外共振随着DDI强度的增加而移动得更快。但是正确的人以强大的DDI强度消失了。此外，Fano共振也随着DDI强度的变化而出现。

结合上述实验，将两个里德伯原子困在一个腔中的多腔光机械系统可以通过现在或近期的技术来实现。