今天我们谈一位大佬——雅可比，我想，很多搞工程，尤其是做工业运动控制的人应该比较熟，尤其是他的雅可比行列式和雅可比矩阵。
另外，喜欢机器人的朋友可以了解下机器人在这个方面的应用。
卡尔·雅可比（Carl Gustav Jacob Jacobi，1804~1851年）,德国数学家
为什么要谈这个人?
首先，我们需要了解这个人的功绩和贡献，需要分析下他究竟通过数学知识解决了一个什么问题？另外，我们会从这个人的视角来看看你不知道一些数学故事。
01 雅可比的数额功绩
卡尔·古斯塔夫·雅可比（Carl Gustav Jacob Jacobi）是19世纪最著名的数学家之一，他在数学领域有着丰富的贡献。
下面是他主要的数学成就：
1、椭圆函数理论：雅可比对椭圆函数的研究具有开创性。他引入了雅可比椭圆函数，这些函数后来成为解析数论和复变函数理论的重要组成部分。他的这些工作也推动了椭圆积分理论的进展。
2.、雅可比符号：雅可比发明了现在被称为雅可比符号的数学标记，用于表示二次剩余，这一符号在数论中具有重要地位。（了解即可）
3、雅可比恒等式和行列式：他提出了著名的雅可比恒等式，这是对向量场的李括号的一种描述。
雅可比行列式也是他的重要贡献之一，广泛应用于线性代数、微分方程和数学物理中。
雅可比行列式的引入主要是为了解决在多变量微积分中的变量变换问题。
当我们在不同的坐标系统中处理函数时，尤其是在进行积分变换时，需要了解一个坐标系统下的小体积元素如何映射到另一个坐标系统中。
雅可比行列式提供了这种映射的缩放因子，这是理解和计算多变量函数的积分的关键。
4、雅可比-梅尔定理：这一定理是关于偏微分方程的，对于理解多变量函数的临界点非常重要。
5、雅可比最速下降法：这是一个经典的数学最优化方法，被广泛应用于物理学和工程学领域。
6、关于动力学的研究：雅可比在动力学领域的研究，尤其是他关于哈密顿-雅可比理论的工作，为分析力学的发展做出了重大贡献。
7、数论贡献：雅可比还在数论领域做出了显著贡献，包括他对伯努利数和雅可比数的研究。
雅可比的工作为后来的数学研究奠定了坚实的基础，并且对现代数学的许多分支产生了深远的影响。他的理论和方法直到今天仍然是数学、物理和工程学中不可或缺的部分。
接下来，我们重点谈谈雅可比行列式与雅可比矩阵。
雅可比矩阵：它是一个函数的所有一阶偏导数构成的矩阵。
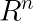
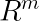
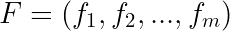
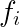
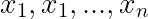
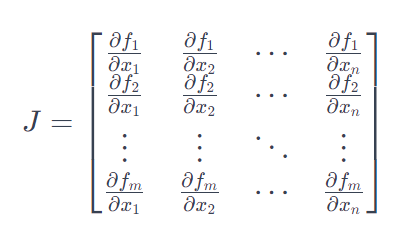
而，当m=n 时，雅可比矩阵是一个方阵，其行列式被称为雅可比行列式。
雅可比行列式提供了一个重要的信息，即这个函数在某一点附近的线性近似的局部伸缩因子。
它在变换坐标系、求解偏微分方程、多变量函数的积分等方面都非常重要。
这里提到雅可比矩阵的目的是为了给大家说清楚，雅可比矩阵在工业机器人领域是一个刚需，我们在做机器人运动学位姿变化的时候必须要用到它，这样有利于计算，尤其是计算矩阵的逆解！
我记得以前大学时候特别想去做机器人，于是去了图书馆，随便翻开一本机器人学的书，才发现密密麻麻全是矩阵，你说学数学没用吗。
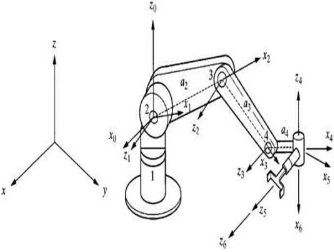
不过话说回来，机器人用的线性代数只是冰山一角，但不可或缺！
关于机器人学由于篇幅原因，有空在工程篇幅我们专门讲，以上不解略过即可。
接下来，我们看看雅可比身边的故事！
02 雅可比的生平
1804年12月10日，卡尔·古斯塔夫·雅可布·雅可比（Carl Gustav Jacob Jacobi）出生于德意志普鲁士的波茨坦，他是富有的银行家西蒙·雅可比（Simon Jacobi）的第二个儿子。
卡尔的第一位老师是他的一位舅舅，他教给这孩子古典文学和数学，为他在1816年12岁时进入波茨坦中学作准备，可以说雅可比的启蒙完全是他舅舅的功劳。
当然，天才总是挡不住的。
从一开始，雅可比就显示出“多才多艺的头脑”，在他离开该校时，中学校长就经常夸奖他。
1821年他离开中学，进了柏林大学。
雅可比像高斯一样，要不是数学更有力地吸引了他，他可以很容易地在哲学上博得很高的名声。
他的教师海因里希·鲍尔（Heinrich Bauer）看出这孩子很有数学天赋，在长时间争论之后，让他自己学习，因为雅可比反对靠死记硬背和规则条例学习数学。
青年雅可比在数学方面的发展，在某些方面很奇怪地与他的更著名的对手阿贝尔相同。
与阿贝尔一样，雅可比也学习大师们的著作，欧拉和拉格朗日的著作教给他代数和分析，并把数论介绍给他。
这段最早的自我教育，必然给雅可比第一项杰出的工作——关于椭圆函数——以明确的方向，因为足智多谋的大师欧拉发现雅可比是他最好的继承人。
就代数中复杂的纯粹运算能力而言，除了我们这个世纪的印度数学天才拉马努金（Srinivasa Ra-manujan）以外，没有人能与欧拉和雅可比相匹敌。
拉马努金
阿贝尔愿意的时候也能像大师一样掌握公式，但是他的天才和雅可比相比，哲学的成分较多，形式的成分较少。
阿贝尔在坚持严格性这一点上，天生比雅可比更接近于高斯——不是雅可比的工作缺乏严格性，它并不缺乏，而是它的灵感看来是形式主义的，而不是严格性的。
虽然这个尝试失败了，但是雅可比从中学到了许多代数知识，他认为这是他的数学教育中相当重要的一步。
他本人在谈到阿贝尔的一篇杰作时说：“它高于我的赞扬，就像它高于我自己的工作。”
当雅可比正在勤勉地使自己成为数学家的时候，阿贝尔已经在将使雅可比成名的同一条路上开了个好头。
阿贝尔在1823年8月4日写信给霍尔姆伯，说他正忙于研究椭圆函数，“这项小小的工作，你会想起来，是涉及椭圆超越函数的反函数的，我证明了一点[似乎是]不可能的东西；我请求尽快把它从头到尾浏览一遍，但是他找不出错误的结论，也不知道错在哪里；天知道我怎样才能让自己解脱。”
一个奇怪的巧合是，雅可比最后下决心要全力从事数学的时候，几乎就是阿贝尔写这封信的时候。
20来岁的年轻人（阿贝尔21岁，雅可比19岁），年龄上2年的差距抵得上成年人20年的差距。
阿贝尔开了一个极好的头，但是雅可比很快就赶了上来，他并不知道他在这方面有一个竞争者。
雅可比第一项伟大的工作是在阿贝尔的椭圆函数的领域内。在注意这项工作以前，我们先概述他繁忙的一生。
雅可比除了自身研究牛以外，他教学生也很出色，尤其是在当数学老师期间发表了一些关于数论的研究成果，惊动了高斯！
因为当时的高斯不是一个容易被惊动的人，教育部立即注意到了这件事，并把雅可比提升到他的许多同事之上，晋升为副教授。
后来，高斯也一直关注雅可比的业绩，并在经济上给予和支持。你可以说他怎么不支持阿贝尔，其实这个问题我也想问。
也许没人知道！
雅可比他是在47岁时死于天花（1851年2月18日）。
在离开这个宽宏大量的人时，我们可以引用他反驳伟大的法国数理物理学家傅里叶的话。
傅里叶指责阿贝尔和雅可比两人把时间浪费在椭圆函数上，而没有在热传导中解决一些有待解决的问题。
总结
历史就是这样，其实指不指责伟大就在这里，我们人类的科技就是在这些点点滴滴的前人的基础上构建而成的。
可以说，没有他们，也许也不会别人发现，只是时间可能慢了点，但是，恰好，也幸好，我们生活的时代很幸福，这就够啦。
