点击关注 关注我们吧~

三角高程测量是在测站点上安置全站仪或经纬仪,观测点上竖立标尺, 已知两点之间的水平距离,根据全站仪或经纬仪所测得的竖直角及量取的仪器高和目标高,再应用平面三角的原理算出测站点和观测点之间的 高差,推求待定点高程。
三角高程测量比水准测量方法更灵活、方便,但测量精度较低,常用于山区的高程控制和平面控制点的高程测定。
一、三角高程控制测量的原理
设在下图已知高程的点 A上安置经纬仪,在B 点上竖立标杆(或标尺),照准杆顶,测出 竖直角α。

设AB之间的水平距离D 为已知,则AB之间的高差可以用下面的公式计算:
h=Dtana+i-v
式中,i 为经纬仪的仪器高度;v 为标杆的高度(中丝读数); Dtana为高差主值。
若 A 点的高程为HA, 那么B点的高程为:
HB=HA+h=Ha+Dtana+i-v
三角高程测量又可分为经纬仪三角高程测量和电磁波测距三角高程测量。电磁波测距三角高程测量常常与电磁波测距导线合并进行,形成所谓的“三维导线”。其原理是按测距仪测定两点间距S来计算高差,计算公式为:
h=Ssina+i-v
电磁波测距三角高程测量的精度较高,速度较快,目前应用广泛。
二、三角高程控制测量中的球气差
由于三角高程测量的计算公式是假定水准面为水平面,视线是直线,而在实际观测时,并非如此。地球曲率和大气折光对三角高 程测量产生的误差。前者为地球曲率差,简称球差,后者为大气垂直折光差,简称气差。

设两差(球气差)的改正数为f:
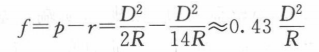
式中 ,D 为两点的水平距离;R 为地球半径,其值为6371km。 球气差改正数可参见下表:

所以,加入球气差改正后的三角高程测量的计算公式为:
经纬仪三角高程测量:
h=Dtana+i-v+f
电磁波测距三角高程测量:
h=Ssina+i-v+f
