​​

这是一道九年级几何题：难度很大，会的寥寥无几，很多孩子无从下手、无奈交白卷！如图一，

图一

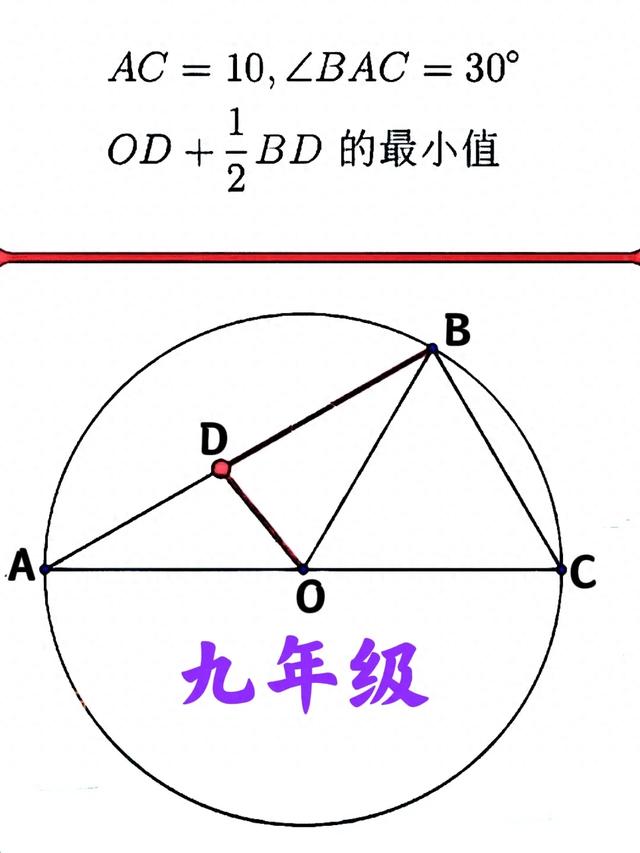
在直角△ABC中，∠BAC=30°，AC=10，D为AB上一动点，点O为△ABC外接圆的圆心，求OD+1/2BD的最小值。

———————————

提示：构造1/2BD+三角形任意两边之和大于第三边！

①过点B作AC的平行线，与圆周相交于点E，则∠DBE=∠BAC=30°，如图二

②过点D作BE的垂线BF，则BF=1/2BD，从而OD+1/2BD=OD+DF≥OF，等号成立当且仅当O、D、F共线，如图二

③过点O作BE的垂线OF'，与AB相交于点D'，如图三

④当点D移动到点D'即点F移动到点F'时，OD+1/2BD取到最小值OF'=√3/2OB=√3/4AC=5√3/2。

————————————

友友们，怎么看？欢迎留言分享！