“数学是宇宙的语言,而数形结合思想则是解锁宇宙奥秘的钥匙。”这句话完美地诠释了数形结合思想在数学中的重要性。在即将到来的中考中,掌握数形结合思想对于解决数学问题有着至关重要的作用。今天,我们将带你一起探索数形结合思想在初中数学中的应用,助你轻松应对中考。
数形结合思想是一种将数学问题与图形相结合的解题方法,它可以帮助我们更直观地理解问题,发现解题的线索。在初中数学中,数形结合思想主要体现在以下几个方面:

1. 函数图像与性质:函数是初中数学的重点内容,通过观察函数的图像,我们可以直观地了解函数的性质,如增减性、对称性等。例如,一次函数的图像是一条直线,其斜率代表了函数的增减性;二次函数的图像是一个抛物线,其开口方向和顶点坐标反映了函数的凹凸性和最值。
2. 几何图形与计算:在几何问题中,通过绘制图形,我们可以更直观地理解问题,发现解题的关键。例如,在解决三角形问题时,通过绘制三角形的图像,我们可以直观地看出三角形的形状、大小和位置关系,从而找到解决问题的方法。
3. 方程与不等式:在解决方程与不等式问题时,数形结合思想同样发挥着重要作用。通过绘制方程或不等式的图像,我们可以直观地看出解的范围和解的性质。例如,在解决一元二次方程时,通过绘制抛物线与x轴的交点,我们可以直观地看出方程的实数根。
下面我们通过三个具体的例子来展示数形结合思想在解题中的应用:
例子1:一次函数的性质
题目:已知一次函数f(x) = 2x + 3,判断其增减性。
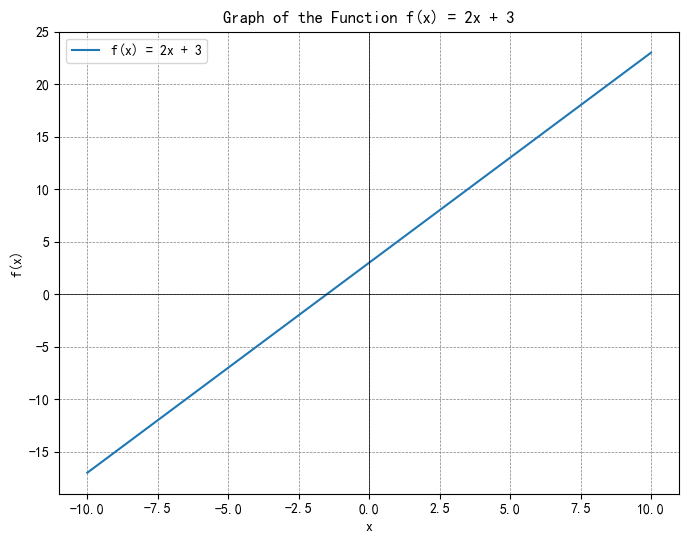
解题思路:如上图所示,这是一次函数 f(x) = 2x + 3 的图像。从图中我们可以看出,这条直线是向右上方倾斜的,这意味着随着 x 值的增加,函数值 f(x) 也在增加。因此,根据一次函数的性质,我们可以判断 f(x) = 2x + 3 是一个增函数。
例子2:二次函数的最值
题目:已知二次函数f(x) = -x^2 + 4x,求其最大值。

解题思路:如上图所示,这是二次函数 f(x) = -x^2 + 4x 的图像。从图中我们可以看出,这个抛物线是向下开口的。要找到这个二次函数的最大值,我们需要找到它的顶点。二次函数的顶点可以通过公式 -b/(2a) 计算得到 x 坐标,其中 a 和 b 是二次函数标准形式 ax^2 + bx + c 中的系数。在这个例子中,a = -1,b = 4。所以,顶点的 x 坐标是 -4/(2*(-1)) = 2。将 x = 2 代入原函数,我们可以计算出最大值:f(2) = -2^2 + 4*2 = -4 + 8 = 4。因此,二次函数 f(x) = -x^2 + 4x 的最大值是 4。
例子3:三角形的角度关系
题目:已知一个三角形ABC,其中∠A = 60°,∠B = 70°,求∠C的度数。

解题思路:如上图所示,我们绘制了一个三角形ABC,其中∠A = 60°,∠B = 70°。根据三角形内角和定理,三角形的三个内角之和为180°。所以,我们可以计算出∠C的度数:
∠C = 180° - ∠A - ∠B = 180° - 60° - 70° = 50°。因此,三角形ABC的∠C的度数为50°。
通过以上三个例子,我们可以看出数形结合思想在解题中的重要作用。它可以帮助我们更直观地理解问题,发现解题的关键。在中考中,掌握数形结合思想对于解决数学问题有着至关重要的作用。希望大家能够通过今天的分享,对数形结合思想有更深入的理解,并在中考中取得优异的成绩!
